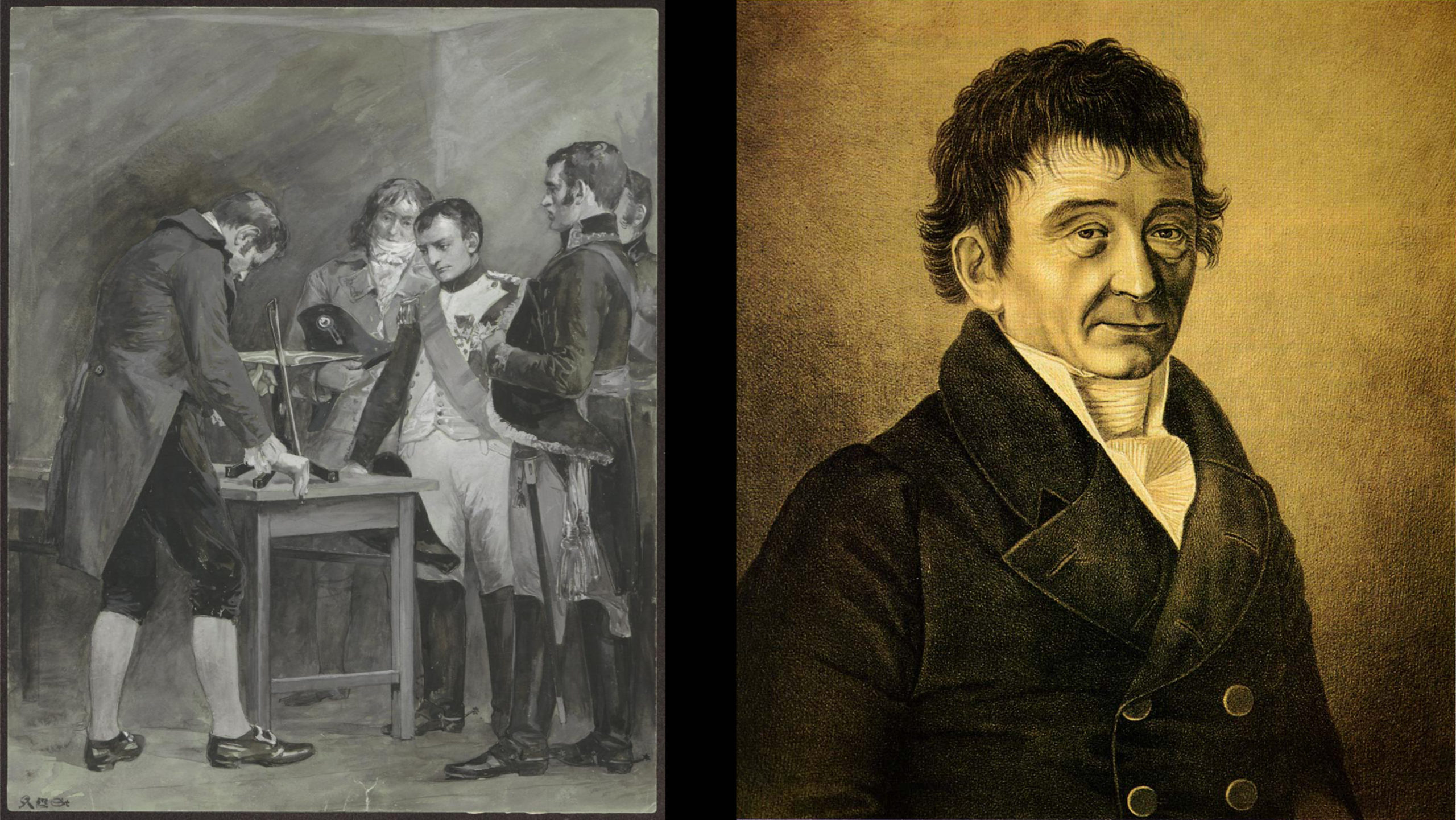de l’Harmonie : la Vibration Originelle

Ἡ.τὸ ἀντίξου ν συμφέρον καὶ ἐκ τῶν διαφερόντων καλλίστη ν ἁρμονία ν καὶ πάντα κατ’ ἔριν γίνεσθαι
Ce qui s’oppose s’assemble, et de ce qui diffère naît la plus belle harmonie,
et la discorde qui engendre toutes choses.
Héraclite, Fragments, VIII

par Patrick Crispini

 télécharger ce texte PDF  –  voir aussi : Sons & Couleurs, des noces inachevées (in revue Terrain N°53)
voir aussi : L’HARMONIE UNIVERSELLE au cœur de la pensée médiévale (Revue Picton-04-2016)

Préambule

Durant toute ma vie j’ai pratiqué et enseigné cette discipline de la musique que l’on appelle : l’harmonie.

On s’y occupe particulièrement de l’organisation verticale de l’écriture musicale, de l’enchaînement des accords, des cadences, en complément du contrepoint, pratique qui s’intéresse plus spécifiquement à la conduite horizontale des lignes mélodiques […]

Au diapason de mes maîtres, qui me transmirent ces connaissances avec amour et conviction, mais d’une manière parfois un peu mécanique, abstraite, j’ai mis toute mon énergie à nourrir l’imagination créatrice de mes jeunes élèves avec ces vieilles règles, qui pouvaient leur sembler surannées, sans vraiment mesurer à quel point les mots et formules de cette matière résonnaient, au-delà de la grammaire musicale et du lexique, à l’échelle de dimensions infiniment plus essentielles – cosmiques – en lien avec les canons de l’univers et les principes les plus fondamentaux contenus dans la matière vivante.

Il m’a fallu une vie entière de musicien pour pouvoir peu à peu libérer la sève métaphysique des consignes et des carcans théoriques, et transmettre à mes étudiants la certitude que la pratique musicale, auquel ils envisagent de confier leur destin professionnel, est bien un ART SUPRÊME, un sésame pour faire de leur être une caisse de résonance de l’univers…

Désormais, avec chaque nouvel étudiant qui me consulte, je m’efforce très vite d’éveiller en lui une curiosité propre à l’usage bien compris de ce mot harmonie, de cette science, plus que musicale : sur une feuille de papier musique, ce ne sont pas seulement des notes, des lignes mélodiques, des rythmes, des structures qui s’assemblent, c’est une philosophie, une métaphysique qui s’organise, une architecture invisible, un savoir vibratoire immémorial…

Tenter de le mieux comprendre est un bonheur à partager : mais le ressentir, à travers le chant, l’instrument, la partition musicale, lue de l’intérieur, est une grâce à vivre !

Un lexique divin

Les mots harmonie, accord, dissonance, consonance, ne sont pas liés par hasard au lexique musical : considérée dès l’Égypte antique et l’école pythagoricienne en Grèce au VIe siècle avant notre ère comme la transcription vibratoire des nombres dans le cosmos – les nombres eux-mêmes portant les proportions de l’ordre universel – la musique est une architecture invisible de l’univers.

Accorder, c’est remplir l’intervalle entre deux termes, deux êtres ou deux choses.

Consonner, pour les Anciens, veut dire demeurer dans l’ordre divin de l’harmonie et du nombre.

Dissonner, par opposition, c’est installer une discordance, une instabilité, qui va nécessiter un réajustement, ce que l’on appelle en harmonie une « résolution ».

Dans résolution, on trouve les syllabes RÉ, SOL, UT, qui sont trois notes de la gamme.

Johannes Kepler, modèle d’univers à partir des cinq polyèdres réguliers de Platon,
in Mysterium Cosmographicum, Tübingen: Georg Gruppenbach, 1596), ETH-Bibliothek Zürich, RAR 1367: 1

Hymne de saint-Jean Baptiste

Ce n’est pas par hasard. Le mot alchimique RESOLUTIO, qui désigne le mystère fondamental de la nature, à savoir la dissolution des éléments dans la mort pour leur reconstitution ultérieure dans un autre ordre, était connu des initiés aux mystères sacrés, et de beaucoup de religieux érudits.

C’est ainsi qu’un simple chant, remis entre des mains avisées, peut contenir à lui seul la cosmogonie secrète d’un message lié à l’harmonie divine, que l’on appelle l’Harmonie des sphères.

En revanche, pour des oreilles non averties, il devient une simple mélodie agréable, sans plus. En outre, élevé à la juste fréquence sous les voûtes d’un édifice capable d’en propager les résonances, il peut manifester de façon transparente le message caché.

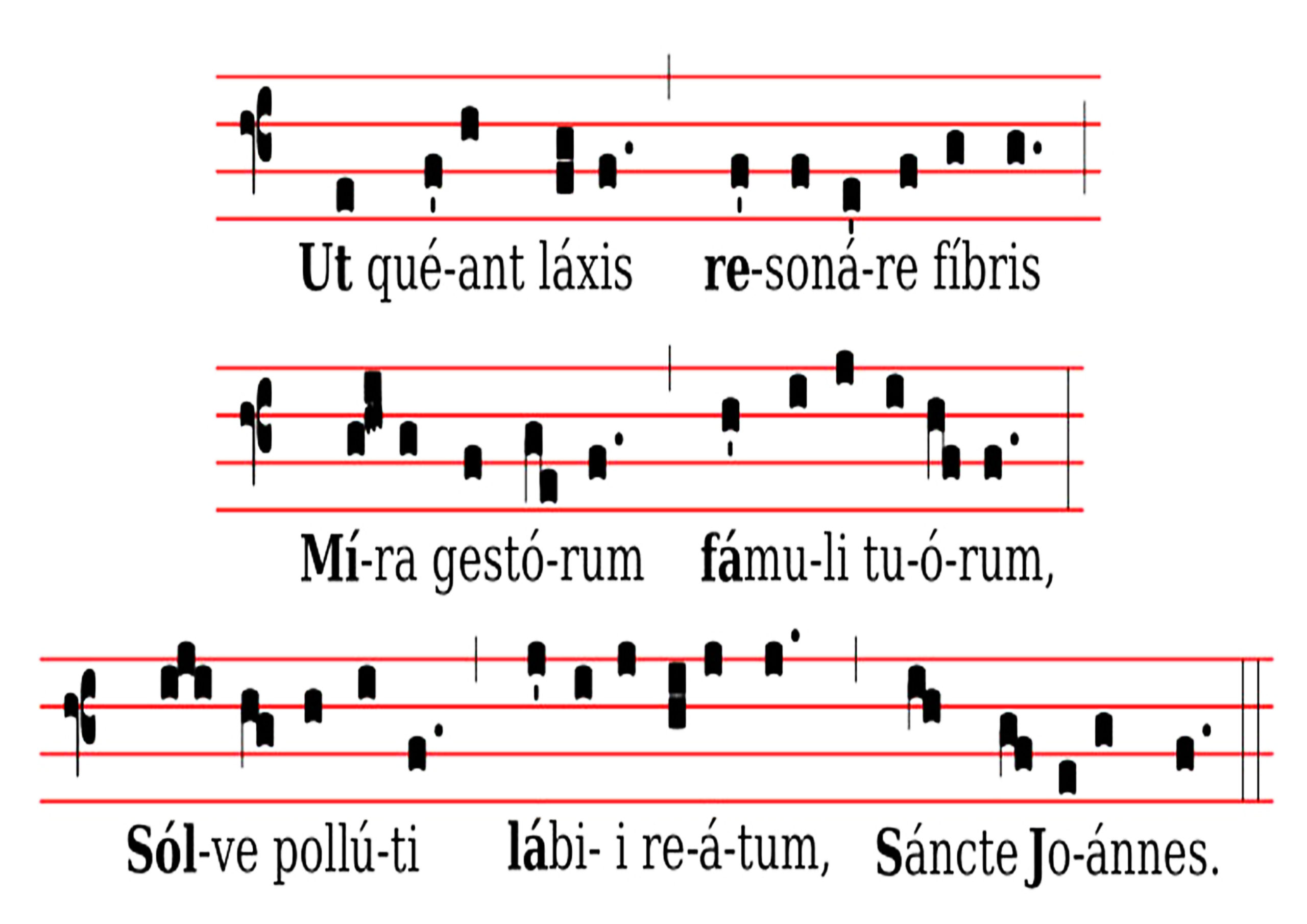
Prenons l’exemple, de l’Hymne Ut queant laxis du moine Paul Diacre, ami de Charlemagne, noté au VIIIe siècle et consacré à saint Jean-Baptiste, dont les premières syllabes forment ce qui deviendra au XIIIe siècle la première gamme musicale occidentale :

Ut queant laxis (do)
Resonare fibris. (ré)
Mira gestorum (mi)
Famuli tuorum. (fa)
Solve polluti (sol)
Labii reatum. (la)
Sancte Iohannes (si)

que l’on peut traduire ainsi :

« Afin que vos serviteurs puissent chanter à pleine voix les merveilles de vos œuvres,
purifiez leurs lèvres souillées, ô saint Jean ».

Que le Baptiste soit porteur du message n’est pas non plus fortuit.
Il est le « récepteur et témoin de la lumière divine ».

En même temps que l’usage de signes musicaux, ou neumes, notés en « campo aperto » (sans ligne), on trouve dès le VIIIe siècle, notamment à Metz ou à Saint-Gall, les premières tentatives de notation sur des portées d’une, puis deux, puis trois lignes, par les chanoines en charge du chant liturgique, afin d’aider les moines copistes à conserver des proportions verticales dans leur graphie.

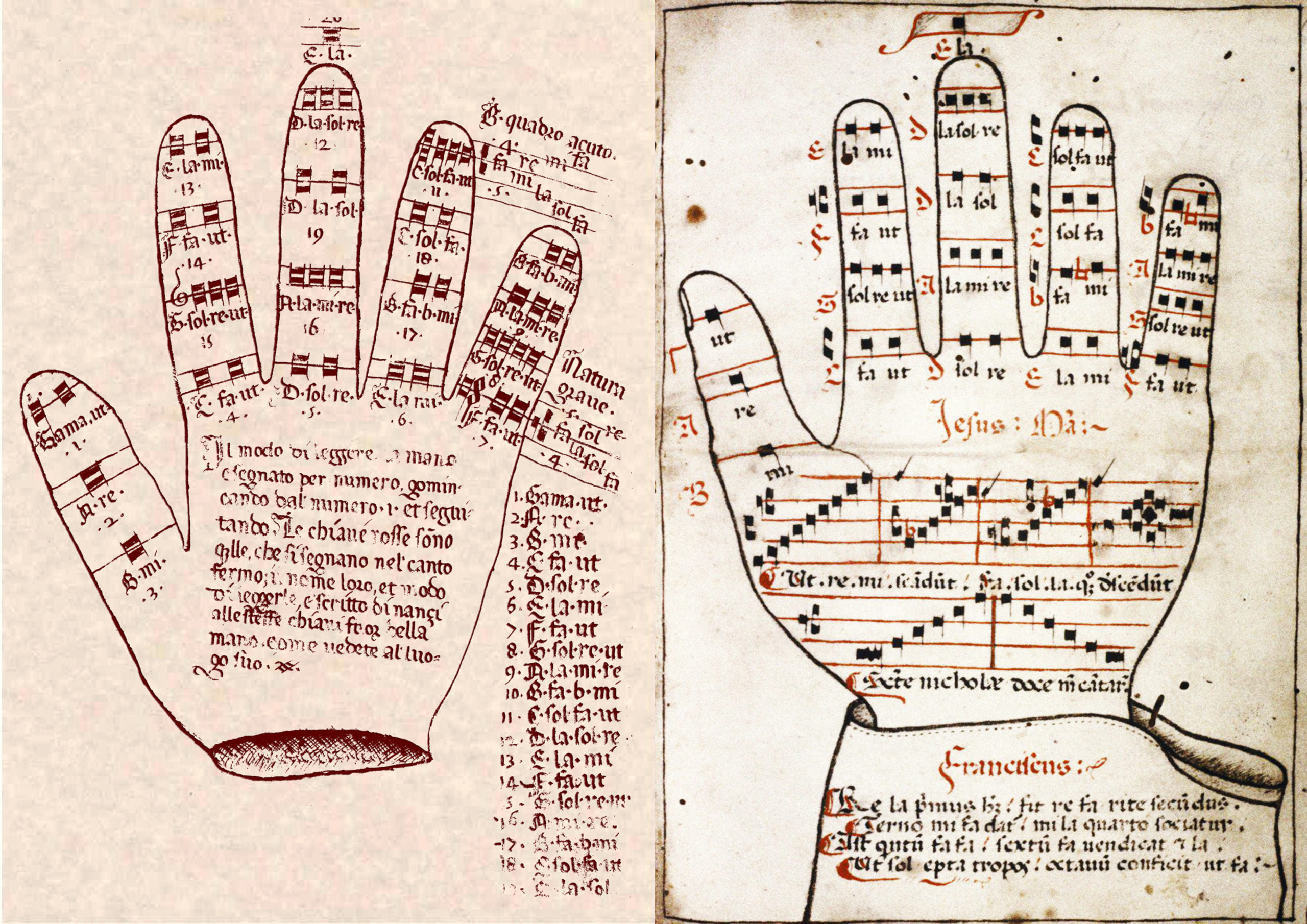
Mais c’est le moine bénédictin italien Guido d’Arezzo (vers 975-vers 1040), qui introduit une quatrième ligne et met au point un moyen mnémotechnique, la « main guidonienne », pour représenter les notes : tous les degrés de l’échelle musicale y sont assimilables aux jointures et aux phalanges des cinq doigts de la main gauche ouverte.

Cette méthode permet aussi de donner des indications aux chanteurs pendant l’office, tout en conservant le silence. Pour son enseignement Guido complète son système par l’usage d’une lettre clef (claves) qui indique la valeur d’intonation, qu’il appelle gamma, d’où le nom de « gamme ».

Deux mains guidoniennes, Oxford University, Bodleian Library , MS Canon. Liturg. 216. f.168 b

Auparavant les notes étaient désignées par les premières lettres de l’alphabet.

Guido se sert désormais des syllabes initiales de chaque vers de l’hymne à Saint-Jean-Baptiste (UT–RE–MI–FA–SOL–LA), le si étant ajouté par Anselme de Flandres à la fin du XVIe siècle et l’ut, jugé trop dur à l’oreille, transformé en do par Bononcini en 1673. Quant à l’origine du mot solfège, elle proviendra des notes sol-fa.
La portée de Guido, étendue à cinq lignes, va se généraliser très vite dans le monde chrétien et devenir la base du système de notation musicale occidentale…

Si l’on écoute maintenant l’hymne lui-même on s’aperçoit que la syllabe SOL, qui en latin signifie « soleil », est à la proportion du nombre d’or dans la continuité du chant, avec sa lettre centrale O.

Cette lettre est la transcription latine de la lettre grecque oméga, dernière lettre de l’alphabet ; jointe à la première lettre alpha (que le Moyen âge orthographie couramment alfa), elle contient la définition que Dieu se donne à lui-même dans l’Apocalypse :

« Je suis l’alpha et l’oméga ».

Dans l’hymne, SOL est encadré par les deux syllabes FA et LA, qui, lues en convergence vers l’oméga du SOL, forment précisément le mot ALFA.

La syllabe précédente MI réunit les deux lettres M et I qui, dans la numérotation alphabétique latine, représentent le plus grand nombre transcriptible (M, mille) et le plus petit (I, un) ; elle est donc une image du macrocosme et du microcosme, représentation de l’univers.

Les deux syllabes initiales du dernier vers, SANcte IOhannes, réunies et lues comme ALFA mais en sens inverse, forment le mot IONAS, nom du prophète qui sortit vivant après trois jours du ventre d’une baleine, et pour ce fait fut considéré comme la préfiguration de la résurrection du Christ, image elle-même de la renaissance printanière après le sommeil de l’hiver.

Si enfin on réunit à SOL et à IO les syllabes UT et RE, on obtient, dans un autre ordre vertical, le mot RESOLUTIO, dont nous venons de parler.

Le groupe RESOLUTIO/ALFA–OMÉGA forme une croix latine régulière :

C’est cette intuition d’un lien universel porté par la musique qui fera dire un jour à Oscar Wilde :

« La musique met l’âme en harmonie avec tout ce qui existe ».

Quant au philosophe rosicrucien Leibniz, dans une lettre à Goldbach datée du 17 avril 1712, il écrit :

« La musique est un exercice d’arithmétique secrète,
et celui qui s’y livre ignore qu’il manie des nombres ».

Une page consacrée à l’Hymne de Saint-Jean dans l’Encyclopédie de Diderot et d’Alembert (1751-1772)
On peut voir que ces principes étaient encore très vivaces au XVIIIe siècle

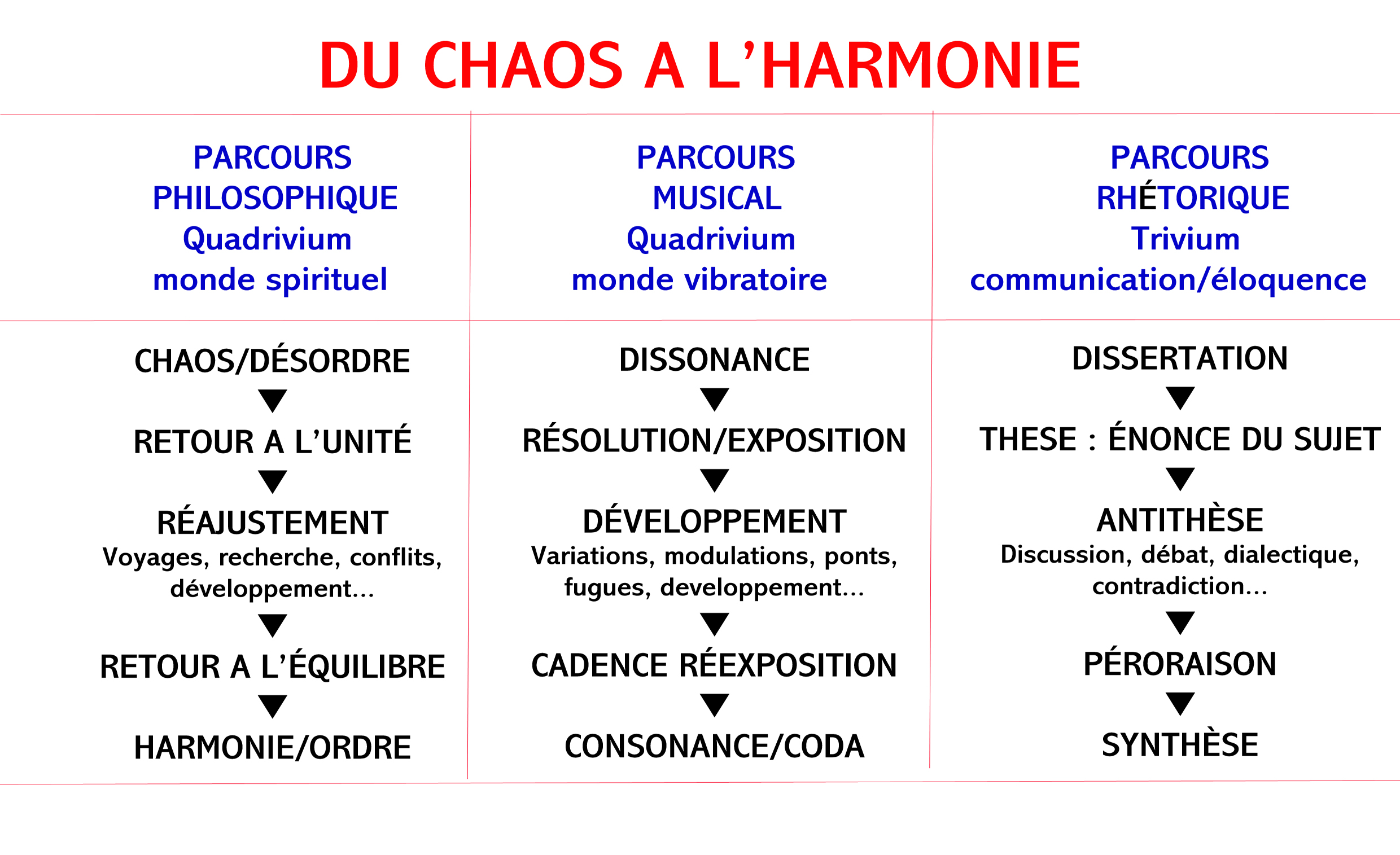
Du chaos à l’harmonie

Il existe bien un lien entre les concepts de chaos et d’organisation. Le premier induit le second, mais ne peut cependant se concevoir que par lui. Cette union, aussi bien présente en musique qu’en astronomie, peut-être élevée au statut de principe universel dans la mesure où on la trouve dans des civilisations pourtant très éloignées.

[…] Dans les anciennes ethnies d’Amérique du Nord et du Pacifique, l’organisation est représentée par un corbeau ; dans les mythologies d’Extrême-orient, l’idée de chaos est souvent représentée par un océan, sur lequel flotte un œuf cosmique, symbole d’organisation.

Il existe dans la banlieue sud de Pékin un temple dédié à l’harmonie du monde, véritable cosmodrome destiné à mettre l’homme en résonance avec le ciel et la Terre. Ce temple a été construit en 1420 et restauré en 1751, soit plus de trois siècles, pendant lesquels l’Europe aura connu les secousses de la révolution copernicienne, les travaux de Kepler, Galilée, Huygens, Descartes, Mersenne et Newton.

La magie de la relativité du temps est ainsi capable d’assurer la pérennité de l’ordre cosmique en extrême orient, tandis que le monde occidental construit laborieusement sa vision universelle, au sein de laquelle l’ordre et le chaos coexistent d’une manière conflictuelle.

« L’harmonie est universellement le résultat de contraires :
car elle est l’unité du multiple, l’accord des dissonances ».
Nicomaque, in De Arithmetica, II

Voilà une définition du mot harmonie, dérivé du grec harmottein (« assembler ») qu’on peut trouver dans l’Arithmétique du néo-pythagoricien Nicomaque, définissant aussi la qualité tout autant morale, esthétique, physiologique, qui découle de choix mesurés par l’équilibre, satisfaisant aussi les principe de proportion à travers la composition des éléments qui l’exprime ou la projette, valable autant pour la musique – qui est la transcription vibratoire du nombre – que pour les autres disciplines de la connaissance. Des termes dérivés s’en font l’écho : harmonieux, harmonique(s), harmonisation, etc.).

Mais le sens global du mot grec est : agrément, union, juste proportion.

On peut immédiatement se poser la question : qu’est-ce qui est juste dans la proportion ?
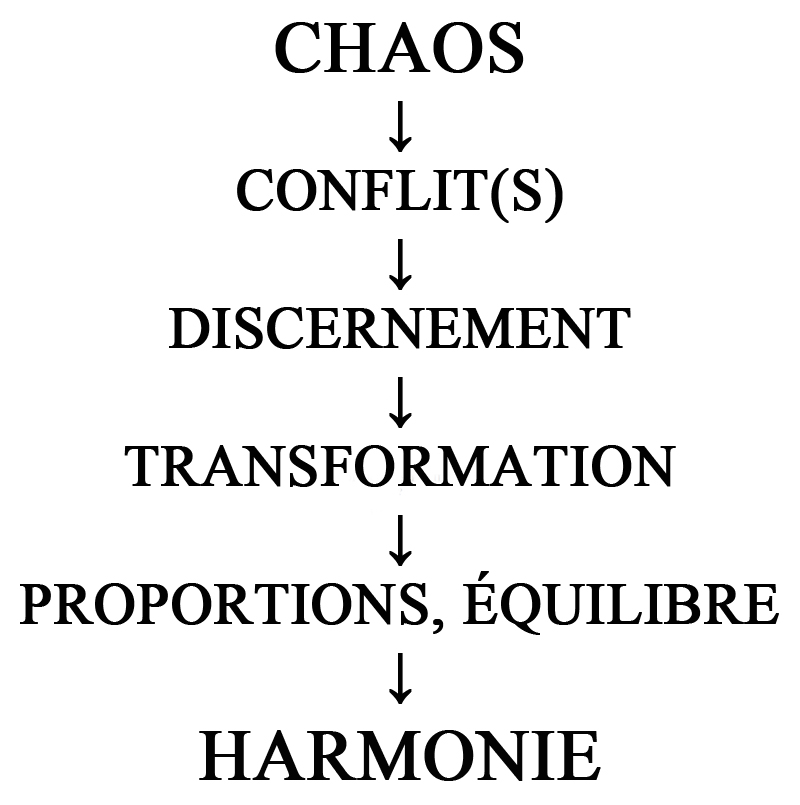
Un idéal, en somme, un concept philosophique, abstrait, au cœur de la matière. Le premier sens étymologique du mot induit aussi l’idée d’emboîtement, de joint, de jointure. Il faut donc, pour qu’il y ait cette osmose, au moins deux éléments, deux forces qui, en se rencontrant, vont devoir s’ajuster en vue d’une fin. La recherche de l’harmonie se situe ainsi au-dessus de celle de l’équilibre, dont la finalité est la stabilité. Ce chemin, du chaos originel à l’harmonie,  peut se résumer ainsi :

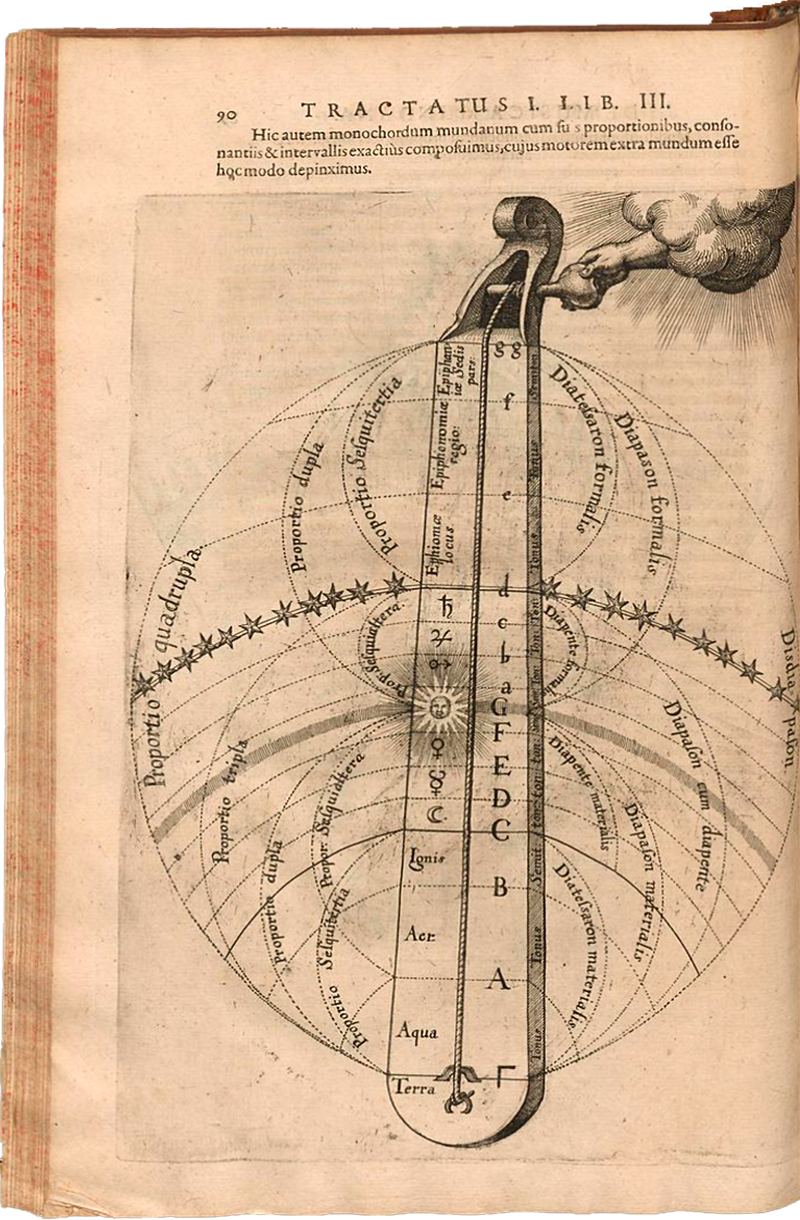
Franchinus Gaffurius (1451-1522), De Harmonia musicorum instrumentorum opus, Milan, 1518

Cette gravure illustre l’enseignement du compositeur et théoricien padouan Franchinus Gaffurius (1451 –1522), dit aussi Franchini ou Franchino Gaffurio, dont Léonard de Vinci fait le portrait en 1490, délivré à 12 étudiants regroupés autour de lui (le nombre, symbolique, évoque entre autres les douze disciples du Christ). Sur le phylactère, à la droite du maître, on peut lire : « Harmonia est discordia concors » (l’harmonie est l’accord issu des contraires), reprenant la formule d’Héraclite : « Ce qui s’oppose s’assemble, et de ce qui diffère naît la plus belle harmonie, et la discorde qui engendre toutes choses » (in Fragments, VIII), elle même relayée par le mathématicien Nicomaque de Gérase « L’harmonie est universellement le résultat de contraires : car elle est l’unité du multiple, l’accord des discordances » (in De Arithmetica, II).

Le principe ORDO AB CHAO – l’équilibre issu du chaos – est contenu dans l’étymologie du mot harmonie, du grec harmottein (« assembler »), qui signifie la juste proportion, après le rassemblement des contraires.

Devant ses 12 disciples (douze est le nombre de l’équilibre et de l’achèvement dans les systèmes numériques), Franchinus évoque les rapports de proportions entre les disciplines de la musique (symbolisé par les divisions des tuyaux d’orgue, à gauche) et de la géométrie (le compas et la division des droites, à droite), le savoir délivré par le maître reposant sur la lumière et le temps (la lampe à gauche et le sablier à droite sur la chaire).

REISCH (Gregorius), Margarita philosophica, totius philosophiae rationalis et moralis principia
XII libris dialoge complectens, Argentorati, 1504, Harvard University

Le chartreux Gregor Reisch (vers 1467-1525), ami d’Érasme et confesseur de l’empereur Maximilien d’Autriche, publie la Margarita philosophica (La Perle philosophique) en 1496 (réimpression 1504), première encyclopédie imprimée en latin qui rassemble l’ensemble des enseignements du savoirs théorique et pratique.

Le mot « margarita », évoquant la marguerite, (de margarite, margerie = perle) symbole alchimique de la lumière révélée après avoir été dissimulée (l’huître).

Sur cette illustration de l’ouvrage on peut voir Boethius (Boèce, à gauche) et Pythagore (à droite) confrontant leurs calculs sous l’égide de Dame Arithmetica. Boèce effectue ses opérations par l’usage des nombres arabo-indiens, issus des graphes sémitiques assyriens, alors que Pythagore utilise l’abaque gréco-phénicien…

Quelle que soit la méthode, le nombre demeure souverain !

Discordia/concors – concordia/discors

L’Harmonie exige en plus une convenance entre des parties initialement opposées ou dissemblables qui suscite un bien-être, une qualité, un épanouissement. Il n’y a donc pas d’harmonie sans conflit, sans divergence préalable.

La concordia est par essence discors. Ce concept philosophique, dont on trouve des traces fécondes dès Horace, notamment lorsqu’il décrit la pensée d’Empédocle dans son premier livre, évoque un monde généré par d’incessantes luttes entre les quatre éléments, où finirait par émerger, grâce aux vertus de l’amour (Aphrodite), une harmonie discordante, née de ces conflits préalables.

ORDO AB CHAO
(l’ordre issu du désordre)

On retrouve cette notion reprise par les Romains : Vénus (équivalent de la déesse grecque Aphrodite), qui symbolise l’amour, la séduction, la beauté, est la mère d’Éros (dieu de l’amour), et du héros Enée, ainsi que l’épouse de Vulcain (l’Héphaïstos grec), dieu forgeron de la métallurgie… qu’elle trompe avec son frère Mars, dieu de la guerre, équivalent d’Arès. L’union, entre Vénus et Mars (l’amour et la guerre) va créer une harmonie discordante, qui ne pourra se résoudre que dans la paix retrouvée.

C’est pourquoi le mot HARMONIE, dérivé du grec harmonia, signifie arrangement, ajustement, et désigne plus précisément la manière d’accorder la lyre (voir l’orphisme).

Ainsi on peut voir que le principe d’harmonie se distingue de celui d’équilibre (aequus, égal, et libra, balance).

Dans la quête de l’équilibre, il n’y a pas d’autre fin que la stabilité, que l’annulation des forces les unes par les autres. On ne recherche pas la fusion intime des éléments, mais leur compensation mesurée, pesée. Si l’équilibre demeure fragile, toujours à surveiller, à recalculer, dépendant de la pesanteur, l’harmonie, à partir du chaos, « travaille » à installer un état durable, dont l’équilibre n’est qu’une des voies préalables.

Python , cratère en calice à figures rouges, vers 350 – 340 avant J.-C., Sant’Agata de Goti (Campanie),
Paestum @ Musée du Louvre, Paris.

Cadmos, futur fondateur de Thèbes, qui combat le dragon ayant tué ses compagnons. est entouré de femmes richement vêtues (personnification de Thèbes et Harmonie, l’épouse du héros). Dans la partie supérieure du vase, quatre figures : Hermès, Aphrodite, mère d’Harmonie, Pan et un satyre.

Aux sources du mythe

L’histoire du mythe autour d’Harmonie, la reine de Thèbes, contient beaucoup d’enseignements. Or les mythes, comme les symboles, contiennent, eux aussi, la métaphore d’un message « subliminal », qu’il faut prendre le temps d’essayer de décrypter.
Rappelons, succinctement, l’histoire de la légende.

Harmonia, est la fille d’Aphrodite et d’Arès. Élevée chez le roi de Samothrace, elle est accordée au prince phénicien Cadmos, qui passe dans l’île, à la recherche de sa sœur Europe, enlevée par un taureau blanc. L’oracle demande à celui-ci de trouver une vache portant sur son flanc un signe en forme de lune et de construire une cité à l’endroit qu’elle aura choisie pour se reposer. Il trouve l’animal dans les troupeaux de Pélagon, le roi de Phocide, qui le conduit près du fleuve Asopos, à l’emplacement de Thèbes. Un dragon, enfant d’Arès, dévore les hommes partis chercher de l’eau pour préparer le sacrifice de la vache. Cadmos tue le monstre. Il devra servir Arès pendant huit ans pour se faire pardonner du meurtre de son fils et devient ensuite roi de Cadmée grâce à Athéna.

Zeus lui donne alors la main d’Harmonie. Des noces somptueuses ont lieu : les Muses et les Grâces y chantent le célèbre épithalame, dont le refrain dit : otti kalon, filon esti, « le beau est aimable ».

Ainsi les dieux vont assister exceptionnellement au mariage d’un mortel avec une déesse et font des cadeaux aux nouveaux époux : Hermès offre une lyre à Cadmos, Déméter du grain et Héphaïstos un collier à Harmonie.

À partir de là le couple va régner en bonne intelligence sur Thèbes. Ils enseigneront l’alphabet phénicien, dont dérive l’alphabet grec, aux Béotiens.

Tentons une première analyse « entre les lignes » : Harmonie est la fille d’Aphrodite – déesse grecque de la Germination, de l’Amour, des Plaisirs et de la Beauté, équivalent de Vénus dans la mythologie romaine – et d’Arès – dieu de la Guerre, de la destruction, lui-même fils de Zeus et de Héra, assimilé à Mars chez les Romains.

Elle est donc le fruit d’une étrange fusion entre des forces créatrices, fécondantes, féminines, et des puissances destructrices, masculines. Son mariage avec Cadmos crée une anomalie dans les règles divines : elle s’unit à un héros mortel, et non pas à un autre dieu. C’est ainsi que l’alliage des forces vitale et guerrière doit se fondre avec la réalité de la vie, pour faire naître la connaissance. En effet, les Grecs attribuent à Cadmos l’invention ou l’importation de l’alphabet et celle de la fonte des métaux.

Pour aider le couple vers ce but, on leur a remis une lyre (la musique), du grain (la fertilité) et un collier, réalisé par Héphaïstos, le dieu du feu et de la métallurgie. Mais ce collier ne peut être porté que par Harmonie : passant de mains en mains, il va entraîner ses possesseurs successifs dans des destins funestes, et même la ville de Thèbes, qui ne s’en relèvera pas.

Descendons encore un peu plus dans les entrailles du mythe.

Il nous enseigne qu’Harmonie ne peut être que le résultat d’une dichotomie fondamentale, et que seul le feu créateur, qu’elle est seule à pouvoir porter, est capable de fusionner en elle.

Portée par la lyre de la musique, qui est la traduction vibratoire et spatiale du nombre, et le grain de la fécondité et de la germination, elle peut ainsi concrétiser l’accès au savoir avec l’aide de Cadmos, par la transmission de l’alphabet. N’oublions pas que la racine sémitique « kad » qu’on trouve dans Cadmos, signifie : celui qui fait briller pour mieux comprendre, et aussi celui qui vient de l’orient, qui montre l’est.

Résumons-nous, une dernière fois : Harmonie ne peut naître que de la maîtrise d’une division initiale (création/destruction), consolidée par le feu de la passion contrôlée (le collier d’Héphaïstos). Mais elle ne peut se suffire à elle-même, étant par définition un idéal presque inaccessible. Pour accéder à la transmission et au verbe (l’alphabet), elle doit s’unir avec l’action (le héros, Cadmos) qui lui montre la bonne orientation : vers l’orient…, tout cela porté par la musique (la lyre d’Hermès), qui est le véhicule secret des proportions parfaites (le nombre).

Comme pour l’Hymne de saint Jean Baptiste, voilà comment une jolie histoire peut dissimuler des vérités autrement plus essentielles. Un sens fort s’en dégage : chacun de nous doit s’efforcer de chercher la créativité dans la transgression et la lutte, et créer sa propre Harmonie à partir des contraires.

« L’harmonie invisible est plus que l’harmonie manifeste », dit Platon.

Voilà pourquoi il faut revenir au nombre et à sa messagère, la musique, pour bien comprendre où réside le vrai sens du mot harmonie.

« La musique est une science qui doit avoir des regles certaines ; ces regles doivent être tirées d’un principe évident, et ce principe ne peut gueres nous être connu sans le secours des Mathematiques : Aussi dois-je avoüer que, nonobstant toute l’experience que je pouvois m’être acquise dans la Musique, pour l’avoir pratiquée pendant une assez longue suite de temps, ce n’est cependant que par le secours des Mathematiques que mes idées se sont débrouillées, et que la lumiere y a succedé à une certaine obscurité, dont je ne m’appercevois pas auparavant ».

Jean-Philippe Rameau, in Traité de l’harmonie, 1722

Pythagore et l’harmonie des sphères

Parmi les mathématiciens pythagoriciens – μαθηματικοί (savants), έσωτερικοί (ésotériques) ou sindonites (habillés du linceuil, placés de l’autre côté du voile), qui sont admis à l’enseignement par symboles (σύμβολα) dispensé par Pythagore derrière son rideau, eux-mêmes subdivisés en σεβαστικοί (pieux), politikoi (politiques) » ou contemplatifs, qui étudient l’arithmétique, la musique, la géométrie, l’astronomie, disciplines qui forment le Quadrivium, largement enseigné pendant tout le Moyen-âge jusqu’à la Renaissance – la transposition des lois harmoniques à l’ensemble de l’univers est essentielle, puisque tout le créé procède du nombre (le mot cosmos signifiant ordre).

Les Pythagoriciens conçoivent un monde achevé, organisé, structuré, à partir d’une matière initiale recouvrant l’Inachevé, selon la déclinaison suivante :

• 1, unité ou monade (1 point, système ou rythme unitaire)
• 2, dualité ou dyade (une droite ou 2 points, système ou rythme binaire)
• 3, trinité ou triade (un triangle ou 3 points, système ou rythme ternaire)
• 4, tétrade (un carré ou 4 points, système ou rythme quaternaire
• 5, pentade (un pentagone ou 5 points, système ou rythme quinaire).

Ensuite viennent l’hexéade, l’heptade, l’ogdoade, l’ennéade et la décade.

On y trouve clairement énoncé l’idée d’un chaos originel qui aspire à l’ordre vers une harmonie potentielle, formulée par les nombres et leurs proportions projetées dans l’univers, exprimée par la transcription vibratoire des sons, de la musique. Il s’en suit que la première métaphysique s’élabore par la pratique de recherches musicales, les pythagoriciens appliquant l’arithmétique à l’étude des phénomènes naturels.

Pythagore va émettre les premiers principes de proportions mathématiques liées aux sons, reprenant des travaux déjà entrepris dans des civilisations antérieures, et qui vont se développer du VI^e siècle avant notre ère, via l’astronomie, les systèmes géocentriques (la terre est au centre du cosmos), les doctrines héliocentriques (le soleil devient le centre de l’univers) jusqu’à l’actuelle « théorie des cordes », dont la physique moderne se préoccupe de plus en plus en ce moment. Pythagore découvre dans les nombres l’explication de l’univers, et dans la science des nombres l’accès au divin, ainsi que l’assurance de félicité éternelle que cherchent mystères et cultes orphiques.

Tout commence, dans la parabole que nous transmet la légende pythagoricienne, par un passage par le feu (toujours le chaos initial !) : c’est, en effet, en passant devant une forge que Pythagore est séduit par un équilibre sonore engendré par la frappe des marteaux des forgerons sur les enclumes.

Pythagore (Tubalcaïn) notant la cognée des forgerons, détail, in Speculum humanae salvationis
(Miroir de l’humaine rédemption), Augsburg, vers 1472.

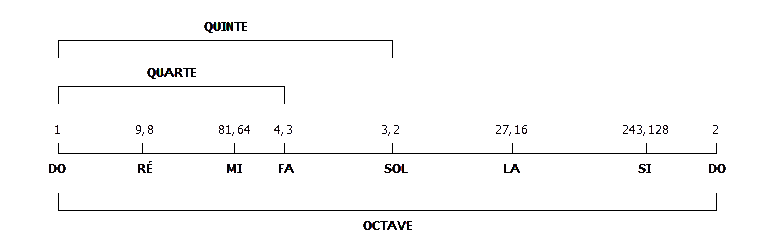
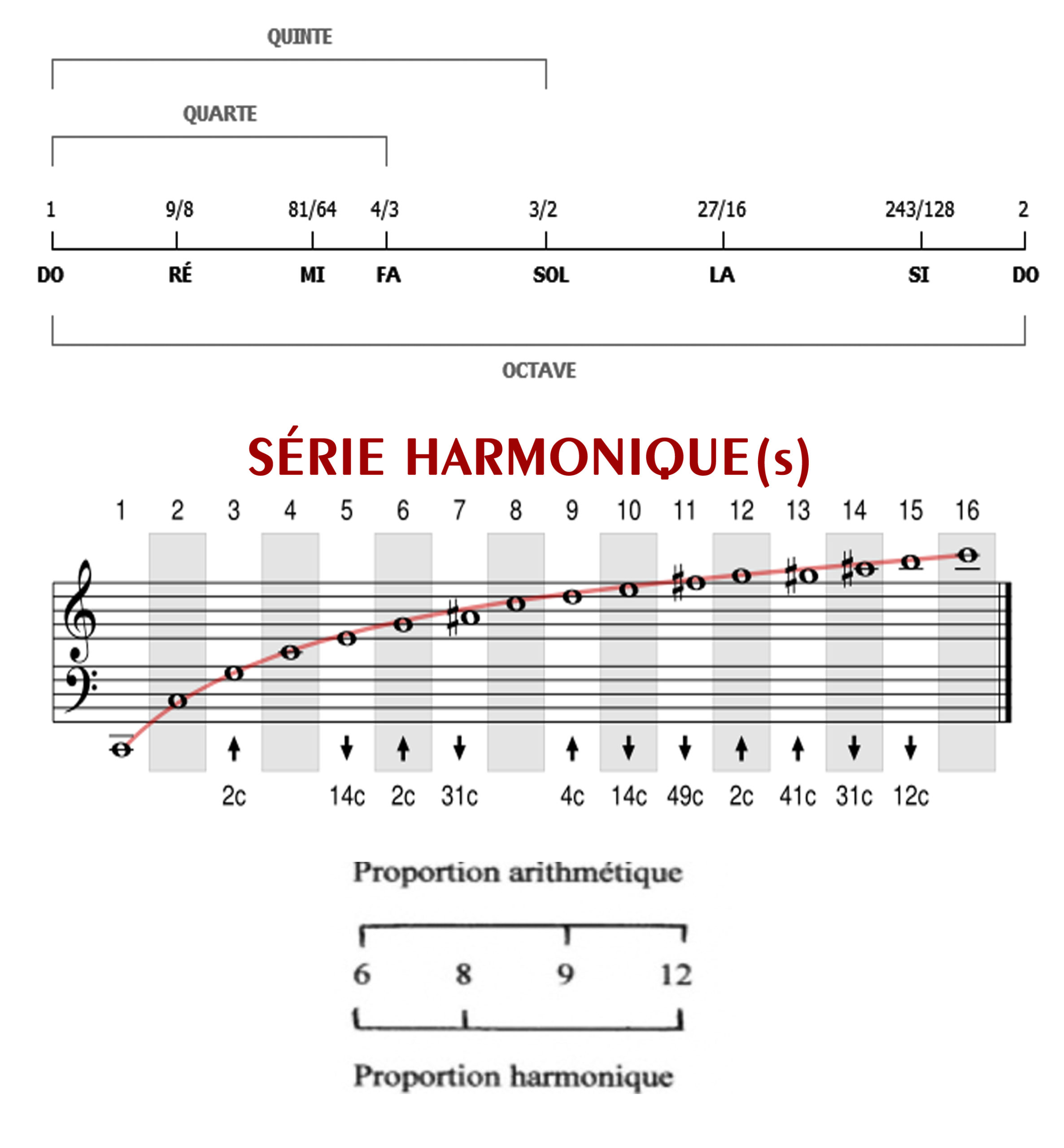
En soupesant les marteaux, Pythagore constate qu’ils pèsent respectivement des poids proportionnels de 6, 8, 9 et 12 et que ces proportions semblent gouverner les intervalles musicaux plaisant à l’oreille. Dans la proportion harmonique 12, 8 et 6, le rapport 12/6 = 2 correspond à l’octave, le rapport 8/6 = 4/3 à la quarte, le rapport 12/8 = 3/2 à la quinte. Il s’en suit que la gamme pythagoricienne va être conçue à partir des intervalles de quintes justes, dont le rapport de fréquences vaut 3/2.

Ainsi les fréquences pythagoriciennes de la note Do sont les suivantes : 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048…

De là va naître la perception des harmoniques, résonnant à partir d’un son fondamental et formant une série de fréquences, multiples entiers de la fréquence du son initial : le 2^e harmonique, ou son 2, sonne à l’octave supérieure du son fondamental, le nombre de vibrations dans un temps donné étant deux fois plus grand ; le 3^e harmonique, ou son 3, sonne à la douzième juste du son fondamental, le nombre de variations en étant trois fois plus grand, etc.

Voilà comment Guido d’Arezzo [~992-~1050], le moine bénédictin à qui l’on attribuera l’invention des notes de la gamme et de la solmisation, rapporte l’évènement au dernier chapitre de son Micrologus, vers 1025 :

« Un certain Pythagore, grand philosophe, voyageait d’aventure ; on arriva à un atelier où l’on frappait sur une enclume à l’aide de cinq marteaux. Étonné de l’agréable harmonie (concordiam) qu’ils produisaient, notre philosophe s’approcha et, croyant tout d’abord que la qualité du son et de l’harmonie résidait dans les différentes mains, il interchangea les marteaux. Cela fait, chaque marteau conservait le son qui lui était propre. Après en avoir retiré un qui était dissonant, il pesa les autres et, chose admirable, par la grâce de Dieu, le premier pesait douze, le second neuf, le troisième huit, le quatrième six de je ne sais quelle unité de poids. Il connut ainsi que la science de la musique résidait dans la proportion et le rapport des nombres ».

Franchinus Gaffurius/Franchino Gafurio (1451-1522), Theorica musiche, Naples,1480.
Démonstration de la légende de la découverte des proportions musicales, de Tubal à Pythagore.

Avant lui le néoplatonicien Boèce [470-525], dans son Institutione Musica de 510, avait déjà raconté la suite de l’expérience :

« Puis il attacha à des cordes (nervis) des poids (pondera) correspondants et discerna à l’oreille leurs consonances ; puis il appliqua des proportions (proportiones) doubles, médianes ou autres à des longueurs de tuyaux (longitudine calamorum) et conçut une assurance parfaite dans ces diverses expériences. En les mesurant, il versa des quantités d’eau correspondantes en poids dans des verres ; et il percuta ces verres, arrangés selon les différents poids, avec un bâton de cuivre ou de fer, en se réjouissant de constater que, là non plus, rien ne divergeait. Ainsi conduit, il se tourna pour les examiner vers la longueur et l’épaisseur des cordes. C’est de cette façon qu’il trouva la règle [regulam, au double sens de la norme et de l’instrument de mesure en bois qu’est le monocorde] ; […] ce type de règle donne une vision (inspectio) tellement fixe et ferme que nul, parmi ceux qui cherchent (inquirentem), ne peut être induit en erreur… »

Boèce est une passerelle essentielle dans la transmission de la culture grecque dans le monde latin, au moment où s’accomplit la chute de l’Empire romain d’Occident, comme le relève Cassiodore, secrétaire des rois ostrogoths en Italie, dans une lettre qu’il adresse au consul et philosophe :

« Nous savons que tu es rempli d’une ample érudition, et que tu as puisé à la source même de la science les arts que le vulgaire pratique sans les connaître […] Au moyen de tes traductions, on peut lire en Italie Pythagore le musicien, Ptolémée l’astronome ; l’arithmétique de Nicomaque, la géométrie d’Euclide sont entendues des Ausoniens, et le théologien Platon, le logicien Aristote, disputent dans la langue de Romulus […] tous les arts et toutes les sciences que des hommes différents avaient donnés à la Grèce féconde, Rome les a reçus de toi seul »

Cassiodore, Ep. I, 45. (L. J. de Mirandol, La Consolation philosophique de Boèce, Paris, Hachette, 1861

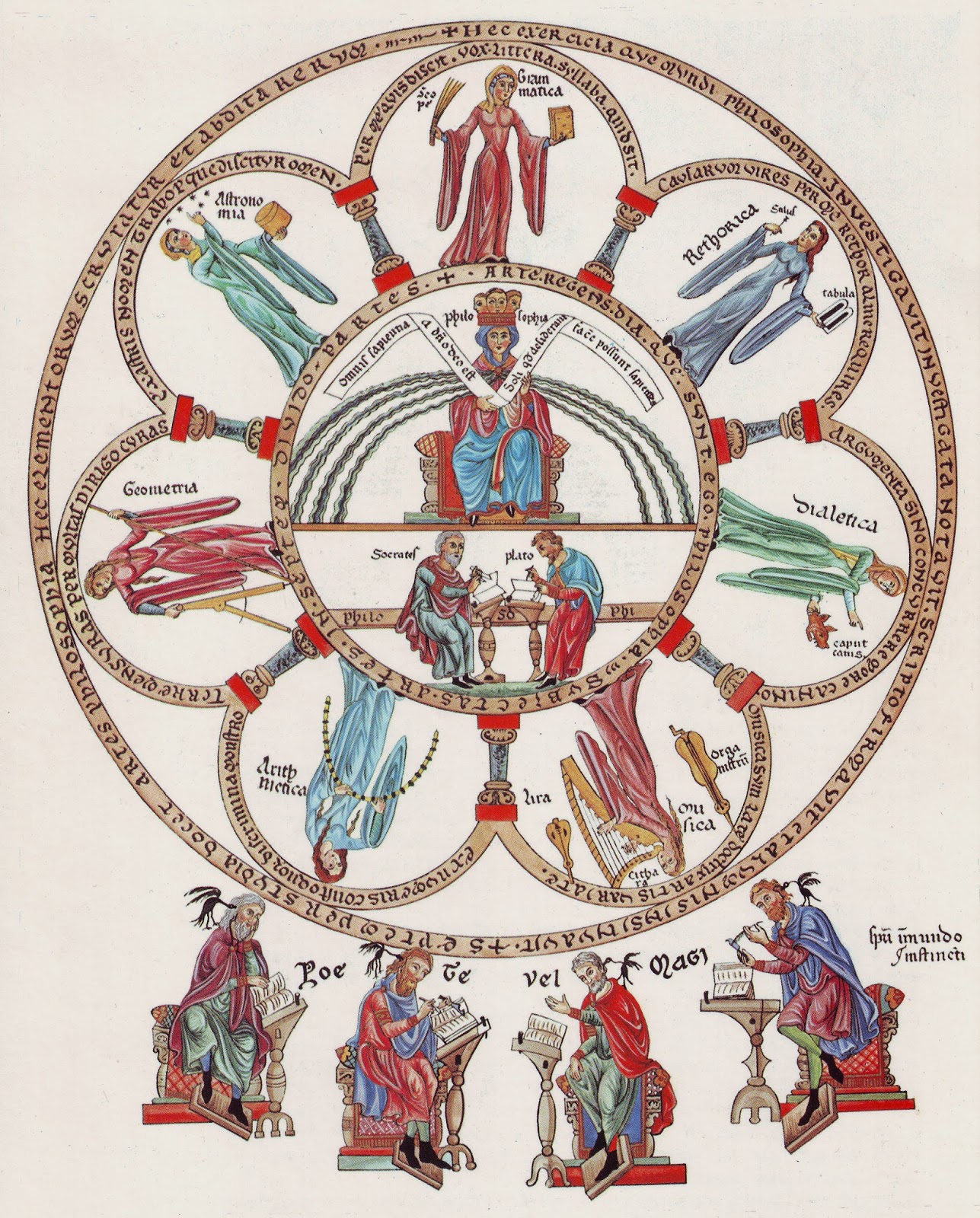
Anicius Manlius Torquatus Severinus Boethius (Rome, ca. 480 – †Pavie, ca. 524), fils de Narius Manlius Boethius (†ca. 487), très tôt orphelin, est recueilli par le platonicien Quintus Aurelius Memmius Symmachus (†ca. 525), duquel il reçoit l’humanitas [παιδεία] (eruditio institutioque in bonas artes), ce qui va faire de lui un homme-université [ὅλως σοϕός], dépositaire d’un vaste savoir [ἐγκύκλιος παιδεία], englobant l’éthique morale, la substantia numeri (science des nombres héritée de Pythagore et de Nicomaque), aussi bien que la summa bona diuina humanaque reposant sur les sept disciplines canoniques des arts libéraux [αἱ ἐλευθέριοι τέχναι], établies par Aurelius Augustinus (De ordine II, 7, 12) et divisées en deux parties distinctes : le Quadruvium (ars arithmetica / ars musica / ars geometrica / ars astronomica) et le Trivium (ars grammatica / ars dialectica-ars logica / ars rhetorica).

Devenu en 520 magister officiorum influent à la cour du roi des Ostrogoths Théodoric (vers 455-526), il sera déchu de sa position par le souverain païen, à la suite du schisme avorté entre Rome et l’église de Constantinople, pendant lequel il est suspecté d’avoir entretenu des liens avec l’empereur byzantin et orthodoxe Justin (vers 450-527). Cette accusation, aggravée par des présomptions de magie, le conduit à la prison de Pavie où, après une longue période de détention, durant laquelle il rédige son De consolatio philosophicae, il est mis à mort en 524.

Boèce constitue donc l’un des traits d’union entre l’Antiquité et le Moyen Âge et doit être considéré comme le « père entre tous du savoir transmis par les anciens » (inter omnes priscae auctoritatis uiros (De institutione arithmetica I, 1).

Son œuvre, tout au long du Moyen Âge et jusqu’aux prémices de la Renaissance, où Boèce jouera un rôle fondamental dans les mouvements de résurgence de la culture antique, notamment à travers Dante et Pétrarque en Italie, Jean Gerson en France, Thomas More en Angleterre, se perpétuera aussi auprès des courants ascétiques et moralistes chrétiens, jésuites de la Contre-réforme, mouvements antitrinitaires aux XVI^e et XVII^e siècles, et jusque dans les ouvrages de Saint-Simon ou Chateaubriand aux XVIII^e et XIX^e siècles, dont on peut mettre en exergue un héritage certain avec sa Consolation philosophique, à la croisée de plusieurs genres littéraires et philosophiques : consolatio stoïcienne et courant ascétique (Sénèque), dialogue à visée didactique (Platon et Cicéron), dialogue intérieur (saint Augustin)…

Anicius Manlius [Torquatus] Severinus Boethius (Roma, ca.480 – †Pavia,ca.524), De institutione arithmetica libri duo |
De institutione musica libri quinque, ca.1130, MS Ii.3.12, fol. 61v, Cambridge University Library

Le Consolation philosophicae, rédigé à l’extrême fin de son existence, alors que Boèce va être condamné à mort, exalte l’inanité des biens terrestres et une méditation sur l’existence du mal, ses origines et les moyens humains pour tenter de s’y soustraire. La question d’où vient le mal (unde malum), reprend celle de saint Augustin dans le Livre VII des Confessions.

Écrite sous la forme du prosimetron, elle utilise le prisme du songe, issu de la tradition littéraire autant biblique que païenne, et la notion de Fortune, rejetée par la conception patristique (saint Augustin), enrichissant ainsi une terminologie apte à influencer le langage philosophique et scientifique médiéval.

Quant à l’influence de ses ouvrages théoriques, elle est tout aussi prépondérante.

De institutione arithmetic libri duo et De institutione musica libri quinque développent la doctrine esthétique de la proportion, d’inspiration néo-pythagoricienne, et associent poésie et musique dans une vision cosmologique du monde. Sans doute porté par la volonté de contribuer à l’unification de l’Église chrétienne, préalable à une hypothétique restauration de l’Empire, Boèce s’emploie à corroborer le bien-fondé des notions touchant à la Trinité et la nature divine du Christ, fixées par le Premier Concile de Nicée en 325, par le truchement de la logique aristotélicienne.

Dans le contexte des disputes christologiques, sa définition de la persona, en particulier, deviendra une valeur fondamentale dans l’histoire des dogmes du christianisme.

L’enseignement de Boèce, basé sur l’étude des concepts fondamentaux et métaphysiques – l’animae generatio [η της ψυχης γενεσις] (la genèse de l’âme), en rapport avec l’anima mundi (l’âme du monde), la substantia numeri (l’essence du nombre), summa bona (le souverain bien), basé sur le quattuor uirtutes animae (quatuor des vertus de l’âme, comprenant la maîtrise du bonheur, de la souffrance, de la justice et l’injustice), les principalitas unitatis (principes unitaires), le continuo proportio superparticularis (les proportions des fractions liées aux principes harmoniques), le sensuum perceptio et cognitio (la perception sensitive et cognitive), decem categoriae ou decem praedicamenta (les dix catégories primordiales), les quinque uoces (les cinq universaux) – deviendra un compendium essentiel dans la tradition du savoir scientifico-philosophique carolingien, l’alpha et l’oméga transmis par l’érudition monastique et universitaire.

La musique comme illustration cosmologique et labyrinthique (Dédale) de l’amour :
La ballade anonyme En la maison Dedalus, in Berkeley Theory Manuscript (US-BEm 744, fol. 31v).
© Jean Gray Hargrove Music Library, University of California, Berkeley.
Le poème en est le suivant:

Dans la maison de Dédale, enfermée est ma dame, vers qui je ne puis aller, car je n’y vois ni issue, ni entrée par où je puisse à son beau corps parler. D’innombrables soupirs m’étranglent, et dans mon tourment, me contraindront à languir… Si je ne la vois pas, même brièvement, je serais bientôt mort. « En la maison Dedalus enfermee est ma dame vers qui ne puis aler car je ni voi issue ni entree par ou je puisse a son gent corps parler. Dont maint souspir me convient estrangler et en tourment me convendra languir se ne la voy briefment m’estuet morir.

Proportions célestes

L’harmonie musicale consiste donc en un rapport de nombres.

Aristote, dans sa Métaphysique, constate que « ces philosophes remarquèrent que tous les modes de l’harmonie musicale et les rapports qui la composent se résolvent dans des nombres proportionnels ». D’où le dogme pythagoricien :

« les nombres gouvernent le monde,
la musique des sphères célestes aussi bien que celle des sons ».

Le ciel, lui aussi, ne peut qu’être proportions harmoniques.

Corps céleste isolé dans l’espace, lui-même enserré au centre d’une sphère, autour duquel gravitent des planètes distantes les unes des autres, posées sur des anneaux circulaires, la Terre fédère ces planètes selon une hiérarchie fondée sur la mythologie, dans l’ordre suivant :

Terre – Lune – Vénus – Mercure – Soleil – Mars – Jupiter – Saturne – Fixes (étoiles).

La première échelle planétaire est établie en fonction de sa coïncidence avec les intervalles musicaux (sept planètes, sept cordes de la lyre) – et donc selon les rapports harmoniques -, en fixant la valeur du ton comme étant égale à la distance Terre – Lune. Les orbites des planètes, y compris soleil et lune, tournent autour de la terre à vitesse constante suivant les mêmes rapports numériques que la gamme. Le cosmos devenant ainsi un gigantesque instrument harmonique d’origine divine, Pythagore associe une note à chaque planète :

– si (Saturne),
– do (Jupiter),
– ré (Mars),
– mi (Soleil),
– fa (Mercure),
– sol (Vénus) et
– la (Lune).

Peut-être est-il utile de rappeler qu’Uranus ne sera découverte qu’en 1781 par William Herschel [1732-1822], musicien anglais (organiste à la chapelle de Bath) et astronome, Neptune en 1846 et Pluton en 1930.

Cependant, vers 220 ap. J.-C. le médecin chinois Koai Yu Tchu expliquait encore à l’Empereur jaune Hoang Ti, au chapitre du traité So Ouenn consacré à l’Étude du Cosmos :

« Selon l’explication de la genèse que m’a léguée mon aïeul de dix générations antérieures à la mienne, il est dit : dans l’immensité de l’espace, il existe une énergie essentielle, primitive, qui donne naissance à tous les éléments et s’y intègre […] À partir de cette création, neuf planètes sont suspendues et brillent dans le ciel : sept tournent au-dessus de nos têtes […] Au ciel l’énergie n’est qu’une substance abstraite, tandis que sur terre, elle se transforme en une substance physique concrète ».

Petrus Apianus, Cosmographicus liber, 1524, Gallica, Figure 12. Le système géocentrique de Ptolémée.

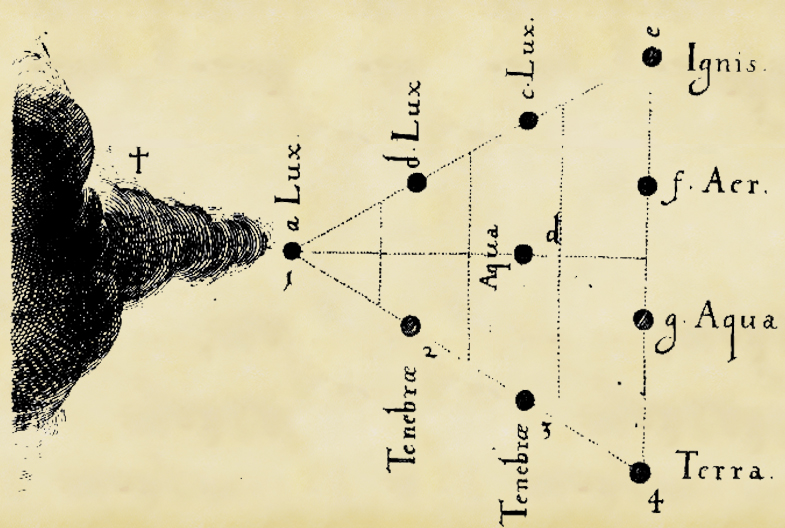
Robert Fludd (1574-1637), Philosophia sacra & vera christiana seu Meteorologia cosmica, 1626
(Philosophie sacrée et vraiment chrétienne, ou météorologie cosmique)

La Tétractys

Dans les communautés pythagoriciennes, l’impétrant (d’abord postulant, puis néophyte), exprimait dans son serment de silence, qui le conduit aux rangs supérieurs d’acousmaticien, puis de mathématicien, ces paroles révélatrices :

« Par celui qui a trouvé la Tétraktys de notre sagesse,
source qui contient en elle les racines de la nature éternelle ».

Le monde sensible révèle son unité dans les nombres et les rapports de nombres dont il est la manifestation. La musique en est l’archétype, et c’est la Tétractys ou Décade de Quatre qui la projette dans la géométrie et l’architecture. Elle est constituée par la somme des quatre premiers nombres : 1 + 2 + 3 + 4 = 10.

Les Pythagoriciens le représentent par le triangle décadique :

Le grand quaternaire est de 36 ; il est formé de 8 nombres, c’est-à-dire par l’addition de la somme des 4 premiers nombres impairs à la somme des 4 premiers nombres pairs, ce qui donne 36. Le quaternaire exprime pour les Pythagoriciens la clef de leur interprétation du monde.

Dans les premières échelles de tons les anciens Grecs positionnent les correspondances planétaires selon ce tableau, où les planètes sont positionnées en fonction de leur vitesse de déplacement vues depuis la Terre, puisque nous sommes ici dans le système géocentrique faisant autorité à l’époque.

Pythagore fait l’hypothèse que tout ce qui est beau dans l’univers, et d’abord l’univers lui-même dans son ensemble, s’explique par des rapports musicaux entre des nombres.

Les Pythagoriciens font l’hypothèse que l’ensemble des intervalles entre les orbites des astres, qu’ils peuvent observer dans le ciel, sont soumis aux lois de l’harmonie de telle sorte que le tout forme une immense lyre aux cordes circulaires produisant des sons agréables : l’harmonie des sphères.

Orphée et la lyre d’Hermès

Hermès (Mercure, chez les Romains) est fils de Zeus et de Maïa, et le messager des dieux.

Il est donc traditionnellement associé au voyage, à l’échange (amoibê) : il conduit les voyageurs et les marchands dont il est le patron, mais aussi les âmes dans l’Hadès, et ne manque pas de protéger au passage les menteurs et voleurs ! L’ingéniosité et l’espièglerie, dont il est doté dès son plus jeune âge, favorisent son habileté : c’est ainsi qu’il va fabriquer une lyre en utilisant une carapace de tortue, puis subtiliser le troupeau d’Apollon qu’il dissimule en le faisant marcher à reculons pour brouiller les pistes. Une fois le subterfuge découvert, Hermès se fera pardonner d’Apollon en lui offrant sa lyre. En échange il reçoit le caducée, qui deviendra un de ses attributs.

L’Hymne homérique à Hermès rapporte ainsi la création de la lyre, v. 20-54 :

« Il [Hermès] trouva une tortue […] La prenant à deux mains, il rentra avec cet aimable jouet. Alors retournant la bête, avec un burin de fer mat il arracha la moelle de vie à la tortue des montagnes. Comme une pensée rapide traverse le cœur d’un homme que hantent de pressants soucis, ou comme on voit tourner les feux d’un regard, ainsi le glorieux Hermès accomplissait ses paroles et ses actes. Il tailla des tiges de roseau à la juste mesure, et les fixa en traversant dans le dos l’écaille de la tortue. Puis, avec l’intelligence qui est la sienne, il étendit sur le pourtour une peau de bœuf, adapta deux bras joints par une traverse, et tendit sept cordes harmonieuses en boyau de brebis. Après avoir si vite construit l’aimable objet, il en éprouva les cordes tour à tour, avec un plectre ; et sous ses doigts la cithare rendit un son merveilleux ».

C’est alors que vient  au monde Orphée. Né des amours de Calliope (« belle voix » en grec) et du demi-dieu Œagre, roi de Thrace, que les légendes représentent souvent comme un dieu-fleuve. Calliope est la plus prestigieuse des neuf Muses, filles de Zeus et de Mnémosyne (la Mémoire) : c’est la muse de la poésie épique et de l’éloquence, celle à qui s’adresse tous les grands poètes pour trouver l’inspiration au moment de chanter, comme l’aède Homère dès les premiers mots de l’Iliade ou de l’Odyssée.

Instruit et parrainé par Apollon, ayant reçu des mains du dieu la lyre d’Hermès à laquelle il ajoute deux cordes (ainsi portées au chiffre de 9, en hommage aux neuf Muses et qu’on retrouvera comme écho aux 9 planètes de l’harmonie des sphères platonicienne), son art tient vite du prodige : aux sons mêlés de sa voix et de la lyre, Orphée envoûte hommes, animaux, rochers et montagnes.

Après de nombreuses tribulations (il aurait participé au voyage de Jason et des Argonautes, mais aussi aurait été initié aux fameux Mystères d’Eleusis…), il rentre et s’installe en Thrace parmi les sauvages Cicones où il épouse Eurydice, une Dryade (nymphe des chênes). Mais, le jour-même des noces, Eurydice, poursuivie par les assauts du berger Aristée, en tentant de lui échapper, bute contre une racine et se fait mordre par un serpent dont le venin envoie la jeune femme au royaume des morts.

Orphée décide de descendre aux Enfers et d’en ramener sa femme. Armé de sa seule lyre, il affronte le passeur Charon, le monstrueux Cerbère, traverse le Tartare où errent les âmes en peine et parvient jusqu’au trône d’Hadès.

L’art d’Orphée est si puissant que les divinités souterraines accèdent à sa demande : il est autorisé à repartir avec son aimée, à la seule condition de faire le chemin sans jamais la regarder tant qu’elle appartient au royaume des morts. Orphée enfreint trop tôt la règle, se retourne et Eurydice, encore dans les ombres, lui est arrachée cette fois-ci, à jamais. Accablé de douleur, Orphée sombre dans un interminable deuil et reste fidèle au souvenir d’Eurydice. Croisant un jour un groupe de Ménades, le poète est attaqué par ces femmes qui, en proie à l’hystérie collective, le tuent et le dépècent. La légende veut que la tête qu’elles avaient arrachée puis jetée à la mer, soit remontée en chantant jusqu’à l’île de Lesbos, terre de poésie. Les Muses ensevelissent Orphée au pied de l’Olympe. Apollon, quant à lui, reprend la lyre et la portera au firmament où elle deviendra une constellation.

Le mythe, comme on peu le voir, est des plus sombres. Il fut prolongé par plusieurs légendes et alla jusqu’à engendrer, au VIe siècle avant J.C, un courant religieux hautement ésotérique – l’orphisme – qui influencera entre autres les pythagoriciens et Platon. Les artistes, quant à eux, vont puiser abondamment dans cette légende où poésie, chant et mort s’articulent en une métaphore édifiante sur l’art. Peintres, compositeurs, poètes, dramaturges et cinéastes en ont fait d’innombrables représentations, interprétations et transpositions.

Alexandre Séon, Lamentation d’Orphée, vers 1896 © Musée d’Orsay, RMN Grand-Palais, Paris

La figure orphique prend trois dimensions essentielles :

• Le poète (musicien-magicien),
• Le prêtre (ou l’initié),
• L’amant (le fidèle d’amour).

Le poète est capable d’agir sur la nature, sur les animaux, sur les humains et sur les dieux eux-mêmes. S’il le fait au moyen de son chant et de sa lyre, c’est également sa parole qui est efficace et qui revêt un caractère pacificateur. Son art vibre d’harmonies musicales, mais aussi d’éloquence et de charme.

Le prêtre est l’initié d’une religion à mystère. Orphée a voyagé durant sa jeunesse, en particulier en Égypte. Diodore de Sicile nous apprend que durant ce périple, il devint le plus grand des grecs dans le domaine théologique, initiatique, et lyrique. Il est considéré comme l’un des fondateurs des mystères d’Éleusis. Il initie ses compagnons d’expédition (Jason et les Argonautes) aux mystères de Samothrace. Orphée est donc le fondateur d’un culte, mais au delà, il est considéré comme étant à l’origine d’une théologie complète : l’orphisme, qui raconte la naissance du monde tout en donnant des conseils de vie pour acquérir le Salut.

L’amant est certes le malheureux époux d’Eurydice. Mais sa ténacité et sa fidélité induisent l’idée d’un amour plus fort que la mort, d’un amour cosmique qui trouvera, dans les grandes gestes médiévales et les plus belles histoires d’amour courtois un prolongement inépuisable. Mais, plus que tout, l’expérience orphique de l’amour absolu nous rapproche de l’Ordre des Fidèles d’Amour, société secrète de gens de lettres à laquelle appartinrent des esprits aussi éclairés que Dante, Pétrarque, Paracelse ou Marsile Ficin… À l’intersection d’une tradition provençale, à travers troubadours et trouvères, et de celle du soufisme (que les Croisés rapportèrent en occident), les paroles d’Ibn’ Arabi, d’Averroès, des âshiq, ou des Shadhiliyya (mêlant amour et poésie), cette philosophie reprenait en écho le symbole de la lyre d’Orphée, à travers une gravitation mystique autour du  nombre neuf. Dans cette initiation, l’expérience amoureuse était vécue comme une mystique à part entière.

« L’amour absolu, indépendant du cœur, fondé sur la foi, est religion », écrit Novalis dans un fragment philosophique bien connu de 1797.

« Tantôt elle est dans les pleurs, tantôt elle est dans les rires ; tantôt ardente de feu, tantôt vibrante de musique ; tantôt la substance même de l’argile humaine est consumée par le feu de l’amour, et tantôt le luth de prééternité accompagne la psalmodie. Tantôt dans l’ivresse mentale, tantôt dans la lucidité, tantôt abolie à soi-même. Tantôt dans l’angoisse, tantôt dans l’exultation ; tantôt dans la crainte, tantôt dans l’espoir ; tantôt dans la séparation, tantôt dans la réunion. Pas d’étape où faire halte, quand elle est séparée ; pas même de séjour à demeure, lors de la réunion. Voilà ce qui est exigé d’un Fidèle d’amour que Dieu mène en ce monde par les degrés de l’amour humain à l’ascension de l’amour divin ; parce que dans le jardin de l’amour, il ne s’agit que d’un seul et même amour, et parce ce que c’est dans le livre de l’amour humain qu’il faut apprendre à lire la règle de l’amour divin. »

Ṣadr al-Dīn Abû Mohammad Rûzbehân (1128-1209),
in Kitâb-e ‘Abhar al-‘ashiqin, Le Jasmin des fidèles d’amour

Le mythe, une fois encore, nous enseigne la route à suivre : grâce à ses talents de chantre cosmique (musique, poésie), mais aussi d’initié (le prêtre d’Éleusis), Orphée peut transcender l’interdit suprême : aller de l’autre côté du miroir, dans le royaume de la mort. Pour cela, il doit revivre le chaos initial en retournant dans les ténèbres puis, fort de son art (la musique) et de ses connaissances en justes proportions (spiritualité), tenter de retrouver la lumière (l’harmonie) grâce à la puissance de son amour. Pour cela, il lui faut s’extirper de ses propres ténèbres, dont son nom lui-même porte la marque de la destinée :  Orphée vient du grec ορφνη « obscurité de la nuit ».

Jean Marais, Orphée moderne, tentant la traversée du miroir dans le film Orphée de Jean Cocteau, 1950
voir : un extrait du film , la Traversée du miroir : «  Il ne s’agit pas de comprendre, il s’agit de croire »

Spéculations et cosmogonies

Platon (v. 428-v. 347 av. J.-C). reprend la théorie harmonique pythagoricienne.

Dès Aristote (384-322 av. J.-C). se dessine une dualité entre l’idée de règles d’harmonie, très rigoureuses, mathématiques, qui permettent d’atteindre la perfection par la raison, et celle d’un sentiment, d’une expérience vécue de l’harmonie qui fait communier avec le divin.

Sous l’influence stoïcienne, la médecine hippocratique va intégrer elle aussi le principe d’harmonie à sa doctrine.

Platon, reprenant Socrate,  avait écrit dans La République, le mythe d’Er le Pamphylien. dans lequel il relate la croyance dans la réminiscence des âmes, leur transmigration dans une après-vie, où les âmes, humaines, végétales ou animales (panthéisme) connaîtraient souffrances ou récompenses selon le degré de leur sagesse…

Cicéron (106-43 av. J.-C.) lui répond par le Songe de Scipion (Somnium Scipionis), passage du livre VI de son dialogue intitulé De republica, où Scipion le Jeune, également appelé Scipion Émilien (Publius Scipio Aemilianus Africanus Minor), décrit le songe qu’il eut 20 ans plus tôt, en 149 avant J.-C., alors qu’il participait à la 3ème Guerre punique auprès du roi Massinissa, allié des Romains. Guidé par son beau-père Scipion l’Africain (Publius Cornelius Scipio Africanus Maior), vainqueur des Carthaginois menés par Hannibal, à Zama, en 202 avant notre ère, et par son père naturel, Paul-Émile (Lucius Aemilius Paulus Macedonicus), vainqueur des Macédoniens du roi Persée, à Pydna, en 168 avant notre ère, il relate ce rêve au cours duquel il est monté jusqu’aux régions célestes, et pendant lequel lui est révélé que les âmes des hommes politiques méritants, après leur mort, s’élèvent au ciel pour une béatitude éternelle. Dans cette Voie lactée, lieu des âmes (τόπος ψυχῶν, topos psychôn), lui apparaît également neuf sphères gravitant les unes dans les autres englobées par la sphère céleste initiale : on y contemple Saturne, Jupiter, Mars, le Soleil, Vénus, Mercure, la Lune et, au cœur du système, la Terre fixe (géocentrisme), qui exécutent un mouvement circulaire « produisant des sons distincts par leurs sept intervalles » (septem efficiunt distinctos intervallis sonos), l’ensemble de ces sons créant une harmonie (sonitus), au caractère « puissant et doux » (tantus et tam dulcis).

Ce texte célèbre dans toute l’antiquité, truffé de réminiscences d’auteurs grecs comme Platon ou Ératosthène, sera relayé et longuement commenté par Macrobe (Ve siècle après J.-C.), encyclopédiste latin, néoplatonicien, auteur des Saturnales, qui en propose une lecture essentiellement  philosophique.

La pérennité du monologue de Cicéron, outre sa qualité littéraire,  s’explique par son lien avec les principes de l’Harmonie des sphères (Harmonices mundi), dont l’attrait perdurera jusqu’au siècle des Lumières.

(voir plus bas : Mozart et le Songe de Scipion)

Le concept d’Harmonie des Sphères est aussi présent chez les néo-platoniciens (Plotin et Proclus).

Dans son De die natali, daté de 238, l’astrologue romain Censorin reprend les principes de Pythagore, en perfectionnant le calcul des distances astronomiques exprimées en tons musicaux :

• de la Terre à la Lune, un ton,
• de la Lune à Mercure, un demi ton,
• de Mercure à Vénus, un demi ton,
• de Vénus au Soleil, un ton et demi,
• du Soleil à Mars, un ton,
• de Mars à Jupiter, un demi ton,
• de Jupiter à Saturne, un demi ton,
• de Saturne aux étoiles (fixes), un demi ton.

Il y a donc trois tons de la Terre au Soleil, soit une quinte, tandis que du Soleil aux fixes (étoiles) il n’y a que deux tons et demi, soit une quarte. On retrouve cependant six tons (une octave) pour aller de la Terre aux étoiles.

Transmise par les Romains, l’harmonie du monde va aussi enchanter la tradition chrétienne : Séraphins, anges et chérubins remplacent sirènes et muses pour faire entendre des accents célestes : l’harmonie des sphères ne peut être que l’œuvre de Dieu.

« L’homme est enserré dans une harmonie universelle des créatures qui répond à une hiérarchie, à un ordre céleste » assure le moine irlandais Jean Scot, à la suite de Boèce.

Comme un écho lointain de Maât, le principe d’équilibre qui, dans l’Égypte ancienne, ordonne les forces de la vie et dicte l’ordre du monde, l’harmonie universelle est un modèle idéal pour toute œuvre humaine.

Cette quête d’harmonie permet d’élever la musique au même niveau que l’arithmétique, la géométrie et l’astronomie, comme l’écrit Cassiodore vers 550. L’ensemble de ces quatre disciplines constitue le Quadrivium, l’essentiel de l’enseignement classique supérieur professé jusqu’à la fin du Moyen-âge. La musique vient en seconde position, après l’arithmétique, dans cet enseignement : toujours le nombre, la proportion, comme Art royal, suivi du son, comme complémentaire cosmogonique. Ce savoir puise ses racines dans la transmission du  Trivium et du Quadrivium (les 7 arts libéraux), qui fut au coeur de toute l’enseignement médiéval et bien au-delà, jusqu’au siècle des Lumières.

Herrade von Landsberg (vers 1125-1195), Septem artes liberales (les 7 arts libéraux), in Hortus deliciarum, vers 1180
une description détaillée

La concordia mundi (l’harmonie du monde), ainsi que la nomme Marsile Ficin, moine occultiste, un des philosophes humanistes les plus influents de la Première Renaissance italienne, qui dirigea l’Académie platonicienne de Florence en 1459, sera aussi chantée par Dante dans l’Enfer de sa Divine comédie… et Milton dans son Paradis !

(voir aussi : Raphaël et l’École d’Athènes, la synthèse métaphysique)

Persuadés de la perfection de l’harmonie musicale, image de celle de la nature, les hommes de la Renaissance en ont appliqué les rapports de nombres aux autres arts.

On connaît la célèbre figure de l’homo quadratus de Léonard de Vinci. Pourtant, cette image des proportions cosmiques du corps est centrée par rapport au regard de l’artiste ou du spectateur humain. L’harmonie n’est plus pure fusion avec l’ordre de la nature.

Vinci, préoccupé comme nombre de ses contemprains cherchants par les questions touchant aux Harmonices mundi, s’interroge : est-ce que « le frottement des cieux fait son ou non » ? Mais, sceptique par nature, il émet des réserves : « S’il n’y a pas d’air dans les cieux, il ne peut y avoir de son ; mais s’il y a de l’air, les corps seraient usés depuis longtemps. De plus, les corps polis ne font pas de son en frottant et si les deux ne sont pas polis après des siècles de frottement, c’est qu’ils sont globuleux et rugueux : donc leur contact n’est pas continu. Il y aurait alors un vide dans la nature, ce qu’on ne peut admettre puisque la nature a horreur du vide. Enfin, le milieu tourne plus vite que les pôles : il devrait donc être plus usé et après usure il n’y aurait plus frottement et le son s’arrêterait… »

Leonardo da Vinci (1452-1519), Homme de Vitruve (le proporzioni del corpo umano secondo Vitruvio),
dessin plume, encre et lavis, vers 1490 © Gallerie dell’Accademia, Venise

L’Homme de Vitruve, dessin annoté, réalisé vers 1490 par Léonard de Vinci, d’après le traité d’architecture De architectura de l’architecte ingénieur romain Vitruve (v-90-v-15 av. J.-C.), incarne les proportions idéales parfaites du corps humain inscrit dans un cercle (centré autour du nombril) (vision spirituelle) et un carré (autour les organes génitaux), symbole terrestre faisant référence aux quatre éléments (eau, air, feu et terre) et aux quatre point cardinaux. Le dessin est un symbole allégorique emblématique de l’Humanisme, de la Renaissance, du rationalisme, de « L’Homme au centre de tout / Homme au centre de l’Univers », de la mesure et de la représentation du monde, rappelant que la Nature et l’Homme sont régis par la géométrie du Quatrivium.

Reprenant les travaux de Platon et des anciens, Nicolas Copernic (1473-1543) argumente sur l’infini de Dieu et de sa création pour conclure qu’il n’y a pas de centre dans l’infini, donc la Terre ne peut être au centre du monde. Son ouvrage De Revolutionibus publié en 1543 sera mis à l’index en 1616 car il sème les premières bases du modèle héliocentrique. Dans le système de Copernic, le Soleil, placé au centre du monde ne joue qu’un rôle d’éclairage des planètes.

Johannes Kepler (1571-1630) donne au Soleil une fonction motrice qui anime les planètes sur une orbite elliptique. Il recherche en outre l’harmonie des sphères dans l’harmonie musicale, à partir de la vitesse angulaire de chaque astre associée à un nombre de vibrations, en donnant à chaque corps céleste une mélodie de base calculée sur l’excentricité de l’orbite terrestre valant 1/2 ton. Ses résultats font l’objet de Harmonices Mundi publié en 1619.

Dans son ouvrage Kepler, astronome et mathématicien impérial à Prague, utilise les proportions au sein d’une gamme musicale pour représenter les proportions au sein du cosmos. « C’est l’expérience infaillible de l’harmonie entre les évènements terrestres et les changements célestes qui a instruit et forgé malgré moi ma conviction ».

Kepler entend démontrer que les lois de l’Harmonie règnent dans tout le Cosmos à travers des relations harmoniques que l’on retrouve dans la mathématique, la musique, la géométrie ou l’astronomie.

Il prolonge le travail de mesure de l’univers à travers les vibrations sonores entamé par Pythagore. Pour cela il reprend les mesures de la trajectoire de la planète Mars qui avaient déjà été effectuées par l’astronome danois Tycho Brahe, et s’aperçoit que l’orbite de la planète autour du Soleil n’est pas un cercle, mais une ellipse, ce qui induit que le système solaire est dynamique et que la trajectoire des planètes est marquée par deux extrémités, l’une où la planète est la plus éloignée du soleil et l’autre où elle en est la plus proche.« Pour éviter des erreurs, il m’a fallu faire reposer le fondement du Monde pour ainsi dire au centre du Soleil ; cela a entraîné que les lieux du Zodiaque, où les planètes sont les plus proches ou les plus éloignées, ne peuvent plus garder leur nom d’apogée ou de périgée, comme le fait abusivement Copernic, mais ont reçu de moi un nom propre et signifiant : aphélie et périhélie ».

Ainsi les planètes, au lieu de simplement graviter autour du Soleil, s’en rapprochent  et s’en éloignent. Ainsi Kepler énonce-t-il sa 3e loi : le carré de la période de révolution est proportionnel au cube de la distance au soleil (T2=R3 où l’emplacement du soleil est une constante).

Et pour représenter cette loi, il va utiliser la musique : en attribuant des notes aux orbites des planètes.

La Terre, par exemple, forme une orbite très légèrement elliptique, presque circulaire autour du Soleil : il n’y a donc pas beaucoup de différence ni de distance entre ses points extrêmes (périhélie et aphélie). Transposée dans une gamme on obtient un demi-ton. De même sur une corde représentant soit une gamme, soit l’orbite de la terre, la distance qu’il y a dans le demi-ton est la même qu’entre le point où la terre est la plus éloignée du soleil et le point où la terre est la plus proche du soleil.

L’orbite de Mercure se trouve très elliptique et plutôt allongée. Étant donc à la fois très proche du soleil et très éloignée, dans la gamme cela donne une octave plus une tierce. Pour l’orbite de Vénus qui est complètement circulaire, il n’y a plus de point éloigné ou proche, ce qui donne l’unisson…

Chaque planète a donc une note fondamentale caractéristique de sa vitesse lors du passage à l’aphélie (proche du Solei), et plus elle va vite, plus sa note se trouve dans les aigus. La variation de vitesse entre l’aphélie et le périhélie est transposée en variation de son, c’est à dire en un intervalle musical.

Sur cette base, Kepler va modéliser tout le système solaire qui, grâce aux proportions, peut ainsi se trouver contenu sur une portée musicale, les écarts entre périhélies et aphélies apportant aussi une solution pour mieux «  tempérer » la gamme. Ces écarts entre les notes planétaires sont une solution au problème de toute façon insoluble (et profondément musical) de la distance entre chaque note.

Dans cette cosmologie sonore, le rapport entre les vitesses extrêmes doit être harmonieux, c’est-à-dire correspondre à une belle consonance musicale (tierce, quarte, quinte, octave). Mais cette harmonie n’est pas perceptible à l’oreille humaine. Pour obtenir une véritable harmonie céleste, il faut faire résonner les planètes entre elles, dans une sorte de polyphonique astrale. Pour y arriver, après de longs calculs, Kepler compara les vitesses extrêmes de différentes paires de planètes en évitant les dissonances, par des proportions musicales planétaires où chaque rapport entre extrêmes est unique.

Voir aussi : Six exoplanètes orbitent en une harmonie précise autour d’une étoile lointaine
(in Courrier international du 26/01/2021)

Nourris de musique et d’astronomie, les Galilée – le père musicien Vicenze [1520-1591] et fils astronome Galileo [1564-1542] – reprennent les gammes planétaires. Ce dernier établit en 1636 la relation liant la tonalité et la longueur d’une corde ou d’un tuyau d’orgue. Malgré l’importance de ses observations grâce à l’usage de la lunette astronomique, on sait dans quelles circonstances dramatiques il devra abjurer les évidences du modèle héliocentrique.

Le père Marin Mersenne [1588-1648], au XVIIe siècle, découvrira les harmoniques concomitants, en même temps qu’il met au point un clavecin de couleurs, cherchant à relier l’univers des ondes élastiques sonores à celles électromagnétiques de la lumière.

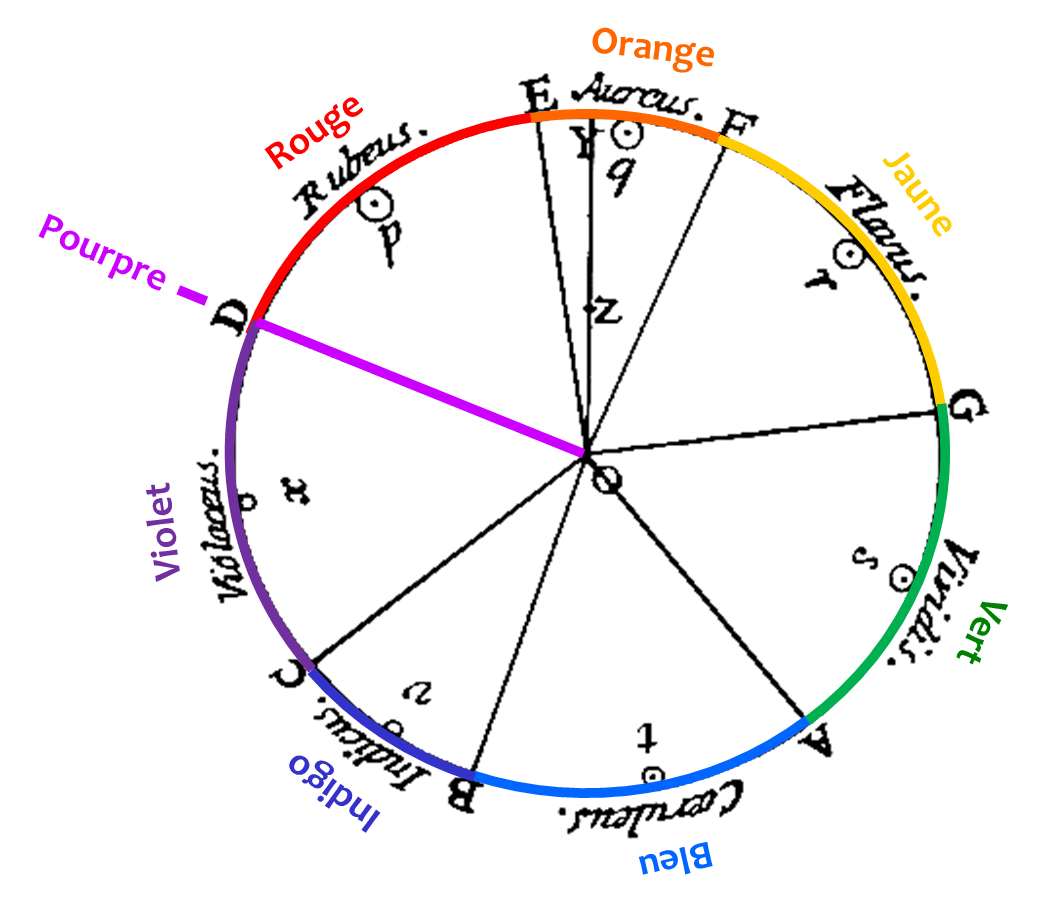
Isaac Newton (1643-1727) en mécanique céleste, observe le domaine visible, l’ordre des couleurs de la lumière et ses limites. L’arc-en-ciel,en particulier, lui révèle l’ordre des couleurs spectrales : aux couleurs « froides » (bleu, vert) succèdent les couleurs « chaudes » (jaune, orange, rouge). Newton va y ajouter la compréhension d’une lumière blanche, composite dont les rayonnements colorés sont les composants élémentaires. Newton les représente sous forme d’un disque reliant ainsi les deux extrémités du spectre. Il insiste sur l’analogie avec la gamme musicale. Ainsi définit-il sept couleurs comme autant de notes se répartissant sur une octave, la continuité perceptive des teintes entre les extrémités violette et rouge se faisant sur la note Ré (D en anglais). Newton n’oublie pas les teintes non spectrales obtenues en mélangeant des couleurs violette et rouge, ce qui donnent le pourpre, axé sur la note Ré.

Newton cherchait à mettre en correspondance les largeurs des bandes colorées que produit la décomposition de la lumière blanche du soleil à travers un prisme et  la longueur des cordes vibrantes capables d’émettre les notes de la gamme diatonique. Pour cet esprit éclairé et spiritualiste, il faut voir là une volonté de conformer sa théorie au principe des Harmonices mundi, faisant fi de tout fondement scientifique. Il n’hésitera pas, malgré sa rigueur scientifique, dans sa théorie des couleurs, à créer de toute pièce une nouvelle couleur intermédiaire, l’indigo, pour que son système reste cohérent avec les principes numériques de l’harmonie des sphères.

Cercle chromatique des couleurs de Newton paru dans son ouvrage Opticks (1704). Les couleurs notées en latin
sont complétées par les lettres A, B, C, D, E, F, G, qui correspondent aux notes la, si, do, ré, mi, fa, sol.
© 2020 LIGHT ZOOM LUMIÈRE, ISSN 2275-1297

[…] Le terrain préparé par Galilée, Kepler, Huygens, Descartes et Mersenne ne pouvait pas tarder à donner une abondante récolte d’idées et de spéculations, largement inspirées des travaux des savants de la fin du XVIIe siècle.

[…] Les conceptions cosmologiques du XVIIIe siècle sont le fruit d’extraordinaires courants de pensée qui circulent à travers l’Europe et se rencontrent dans les pôles d’attraction que sont les cours princières.

Frédéric II (1712-1786), roi de Prusse, hérite de cet afflux d’idées novatrices et fonde son pouvoir sur la raison, en refusant de donner un caractère religieux à l’autorité. Ami de Voltaire et des philosophes, protecteur des arts et des sciences, sa cour est un des foyers culturels et artistiques les plus importants, véritable temple de la connaissance, lieu de rencontres et de confrontations d’idées philosophiques, scientifiques et musicales.

Au sein de cette cour princière, des astronomes comme Maupertuis ou Lambert croisent des musiciens comme les Bach père et fils. L’Histoire générale de la nature et théorie du ciel de Kant est dédié en 1755 à Frédéric le Grand, ainsi que l’Offrande Musicale de Bach, dont la dédicace date de 1748.

Johann-Sebastian Bach, Das Musikalische Opfer, 1747, manuscrit autographe de la fugue du Ricercare à 6 voix,
énonçant le thème royal, détail © Staatsbibliothek zu Berlin

L’Offrande musicale du Kantor

L’intérêt de Johann-Sebastian Bach [1685-1750] pour la métaphysique des nombres a sans doute été renforcé par la fréquentation de son maître, le compositeur et organiste Dietrich Buxtehude [1637-1707] auprès duquel il séjourna trois mois à Lübeck. Danois de naissance Buxtehude s’intéressait beaucoup à l’astronomie, ayant été organiste à Elseneur, à proximité de l’observatoire de Tycho-Brahé [1546-1601]. Illustrant en particulier les quatre phases de la Lune, dont le cycle est de 28 jours, Buxtehude écrivit une Passacaille comportant quatre sections musicales, chacune déclinant sept fois le thème à la basse.

On connaît l’histoire fameuse de la genèse de l’Offrande musicale (Das Musikalisches Opfer)

Le nouveau roi de Prusse Frédéric II, flûtiste de talent, élève de Joachim Quantz, s’essaie volontiers à la composition. Ouvert aux idées novatrices des Lumières, humaniste, « despote éclairé », il nomme, dès son accession au trône, Carl Philipp Emanuel Bach [1714-1788], fils du vieux Kantor, claveciniste de la Cour.

C’est sans doute par l’entremise de ce dernier qu’il va prendre contact avec Bach père, dont la renommée de virtuose et d’improvisateur dans le style ancien l’intrigue. Bach, alors âgé de 60 ans, finit par se laisser tenter, et fait le voyage pour Berlin, où il arrive à Sans-Souci le soir du 7 mai 1747. Le roi lui fait essayer divers instruments à clavier et en particulier les sept piano-fortes de Gottfried Silbermann, dont il est très fier.

La chronique d’Anna Magdalena Bach précise que « Sébastien s’assit, se mit à jouer, et peut-être quelques-uns des auditeurs se rendirent compte que cette nuit-là il y eut deux rois au palais ». Frédéric lui propose ensuite un thème, sur lequel il lui demande d’improviser une fugue à trois voix; puis d’improviser sur le même thème une fugue à six voix. Bach décline alors la proposition, considérant le thème inadéquat, et choisit un de ses propres thèmes pour improviser la fugue.

Mais, de retour à Leipzig, le compositeur s’emploie à transformer son refus en chef-d’œuvre : reprenant le thème royal, il conçoit l’Offrande musicale. Dans l’exemplaire que Bach envoya au roi Frédéric, sur la page de garde se trouve l’inscription :

« Regis Iussu Cantio Et Reliqua Canonica Arte Resoluta », que l’on peut traduire par « morceau réalisé par ordre du roi et autres morceaux résolus suivant l’art du canon », auquel s’ajoute cette préface ironique : « Traiter le thème royal en toute perfection et le faire connaître au monde ! »

Les initiales de l’épigramme latine forment le mot R.I.C.E.R.C.A.R, autrement dit, « rechercher ».

voir : un extrait du film de Dominique de Riva, Mein  Name ist Bach (2004) qui évoque cette histoire.

Là encore le lien avec les Harmonices mundi est évident : il s’agit, par les proportions et le nombre, de refléter l’ordre cosmique qui, dans le cas de Bach, célèbre la présence intangible de Dieu. Soli Deo Gloria (S.D.G. et son équivalent en notes musicales) marque une des signatures favorites de Bach dans ses œuvres, qui « signe » aussi parfois avec la cellule de son propre patronyme : B-A-C-H (si bémol, la, do, si bécarre)…

L’Offrande Musicale se compose d’une fugue à trois voix, d’une autre à six voix, de dix canons et d’une sonate en trio. Bach accordait une grande importance au canon : faisant partie depuis juin 1747 d’une société savante dirigée par Lorenz Mizler, il s’était fait peindre par Elias Gottlob Hausmann avec à la main un feuillet montrant un canon renversable d’une grande subtilité. Chaque canon se présente comme une « énigme » à résoudre, dans l’architecture la plus subtile et la plus ingénieuse.

Elias Gottlob Hausmann (1695-1774), Portrait de Johann-Sebastian Bach, 1748 © Stadtgeschichtliches Museum Leipzig

Le travail en canon permet d’élaborer des architectures musicales d’une certaines complexités : le canon simple, où le thème proposé par la première voix est suivi de sa répétition exacte avant sa résolution ; le canon ad infinitum, circulaire, ou perpétuel, où les voix s’enchaînent en boucle ; le canon par augmentation ou par diminution, où le thème proposé est résolu en valeurs de durées plus longues ou plus brèves ; le canon renversable, le canon rétrograde, dit à l’écrevisse, où la résolution reproduit le thème à rebours en commençant par la dernière note; les canons énigmatiques ceux dont la notation, réduite à une seule portée, ne contient que le thème et indique par des signes et des devises codées la manière de le résoudre…

Avec Bach l’écriture musicale, au-delà de la séduction mélodique et harmonique, contient les ressorts dissimulés d’architectures complexes, combinatoires, où les proportions des nombres et la symbolique numérique jouent un rôle essentiel. Bach appartient encore à cet ancien monde des cosmogonies interprétatives du monde, où la lumière de Dieu tient la place centrale, dans un théocentrisme évoluant progressivement vers l’anthropocentrisme, modulé par l’héliocentrisme copernicien.

Ses propres enfants, eux-mêmes compositeurs, prendront d’ailleurs des distances avec leur père, ce qui les rattache déjà à la nouvelle lecture rationaliste de l’univers, annoncée par l’Aufklärung et les Lumières du XVIIIe siècle, propagée par les salons philosophiques et les cabinets de curiosités des cours princières, les progrès de la facture instrumentale, l’intensification des échanges, la propagation des idées nouvelles par les libelles, la constitution de laboratoires de recherche et le développement des expéditions scientifiques…

Bach conçoit l’art musical comme le territoire de la rationalité des proportions et du nombre, mais aussi comme une architecture métaphysique au service d’une cosmogonie dont la figure de Dieu est l’achèvement.

Il se situe dans la lignée d’un Johannes Kepler (1571-1630), astronome, mathématicien, mais aussi kabbaliste, ou d’un Isaac Newton (1642-1727), chercheur le jour, mais qui pratique le soir des travaux d’alchimie, en même temps qu’il effectue ses recherches en optique et physique.

Pour Bach la beauté sonore doit se dégager d’une forme subtilement élaborée en géométrie et en proportions, de la même manière que l’ordre divin est révélée par le nombre, qui lui-même EST vibration, c’est-à-dire, musique.

Dans le labyrinthe des canons et contrepoints de l’Offrande musicale, ou encore dans la cathédrale testamentaire de l’Art de la fugue, Bach s’en donne à cœur joie pour parsemer le parcours de l’œuvre d’objets sonores à ressort complexe, usant de la forme du palindrome (imitation rétrograde, appelée aussi « à l’écrevisse »), construisant une géométrie de symétries basée sur des axes verticaux ou horizontaux, en renversant les intervalles du motif initial (par exemple, si le dessin mélodique monte d’une quinte, son imitation renversée descend d’une quinte, par mouvement contraire).

Dans le contrapunctus III de l’Offrande musicale, Bach note un canon en mouvement contraire écrit pour 3 instruments, alors que la partition ne comporte que deux portées : le troisième instrument devra lire sa partie « en miroir » !

C’est ainsi que transpositions, imitations, figuralismes mélodiques, porteurs d’une métaphore liée au texte chanté, proportions numériques, parsèment de nombreuses œuvres du Kantor, comme les rébus, anamorphoses ou carrés magiques pouvaient révéler à certains esprits avisés ou « initiés » – dans les œuvres de peintres comme Albrecht Dürer [1471-1528] ou Hans Holbein [1497-1543], par exemple – la vérité des justes proportions, dissimulées sous les apparences trompeuses des portraits et des motifs gravés.

Hans Holbein le Jeune [1497-1543], Les Ambassadeurs, 1533 © National Gallery, Londres.
voir : une description filmée de ce tableau © CED, Canal éducatif, l’Art en question

Nicolas Bion (1652-1733). Figure des Tourbillons Célestes (d’après Descartes), in Usage des globes célestes et terrestres
et des sphères, suivant les différents systèmes du monde, précédé d’un traité de cosmographie… , J. Guérin, Paris, 1751

Les cosmologies de la raison

Dès 1637, dans son Discours de la méthode (1637), René Descartes [1596-1650] avait imposé une cosmogonie « mécanique » reposant sur le principe d’un univers à la fois infini et plein, afin de « parler seulement de ce qui arriverait si Dieu créait maintenant quelque part dans les espaces imaginaires assez de matière pour composer [le monde] et qu’il agitât diversement et sans ordre les diverses parties de cette matière en sorte qu’il en composait un chaos […] et que par après, il ne fît autre chose que prêter son concours ordinaire à la nature, et laisser agir suivant les lois qu’il a établies ».

René Descartes, in Discours de la méthode, 5e partie.

Le modèle est « évolutionniste », à partir d’un chaos initial. La matière reste immuable, tant qu’elle n’en rencontre pas d’autre ; tout corps poussant un autre corps lui induit autant de mouvement qu’il en perd lui-même. Ainsi les particules de terre (plus lourdes) rencontrent-elles celles d’air (moyennes) et celles de feu (plus légères), en s’assemblant en tourbillon, les particules de feu, plus rapides, s’agglomérant au centre de cette masse, telle une étoile, qui se met aussitôt à exercer une pression sur d’autres masses étoilées qui, peu à peu, se recouvrent de matière lourde, qui va, finalement les empêcher de briller, entraînant du même coup la disparition du tourbillon initial. L’étoile ainsi couverte de matière lourde se déplace vers d’autres tourbillons, apte à devenir une planète…

Christian Huygens [1629-1695] dans son Discours sur la cause de la pesanteur de 1690, reprendra en partie la théorie des tourbillons chère à Descartes.

Dominantes à la fin du XVIIe siècle, les thèses cartésiennes commencent à faire concurrence aux Principia d’Isaac Newton [1642-1727], dont la mécanique sophistiquée ne propose pas d’explication structurelle claire à propos de l’organisation et la stabilité même de l’univers, Newton s’en remettant à Dieu pour cette « arrangement » céleste :

« On voit que Celui qui a arrangé cet Univers a mis les étoiles fixes à une distance immense les unes des autres, de peur que ces globes ne tombassent les uns sur les autres par la force de leur gravité ».

Isaac Newton, in Principes mathématiques de la philosophie naturelle, T. II, 1759

Au début du 18e siècle le Deus ex machina de Newton va entretenir la multiplication de traités physico-théologique, qui s’efforcent de concilier les théories de newtoniennes avec une cosmologie issue de l’ordre divin.

Mais de nouvelles spéculations, portées par le rationalisme de l’Aufklärung, annonçant les démarches philosophiques du siècle des Lumières, vont voir le jour. Des chercheurs proposent simultanément, mais souvent de manière indépendante, de nouvelles tentatives d’explications cohérentes de l’univers.

L’astronome et mathématicien britannique Thomas Wright [1711-1786], le philosophe allemand Emmanuel Kant [1724-1804], le mathématicien Johann-Heinrich Lambert [1728-1777] ou le compositeur et astronome anglais William Herschel [1738-1822] vont ainsi contribuer à mettre en place les nouvelles cosmologies, corroborées par le progrès des nouveaux instruments de recherche, de l’optique, l’amplitude des laboratoires scientifiques, l’organisation des astres, les structures et l’origine de l’univers qui émergent au siècle des Lumières.

Dans son ouvrage, publié en 1750, On Original Theory or New Hypothesis of the Universe, Thomas Wright [1711-1786], tout en donnant des cours de navigation dans le port de Sunderland en Angleterre et des conférences devant les membres de la high society, propose une « relecture » des phénomènes astronomiques, rangeant les étoiles en deux catégories : celles qui sont partie intégrante de la Voie Lactée et les autres en dehors, tout cela, en perpétuel mouvement circulaire, plutôt que rectiligne, s’organisant dans un plan d’ensemble unique, mais où la place centrale du soleil, selon la révolution copernicienne, est remise en cause, au nom de la subjectivité même de notre situation d’observation, qui nous fait voir une partie infime du système, mais non l’architecture globale de l’univers.

« La Terre (…) a longtemps été le principal lieu de notre système, et y régnait paisiblement, comme au centre de l’Univers, durant plusieurs époques du passé ; mais c’était une ignorance humaine, et non une sagesse divine, qui la plaçait à cet endroit (…). Maintenant elle n’est plus du tout le seul globe terrestre dans l’Univers ».

Thomas Wright, in On Original Theory or New Hypothesis of the Universe, London, 1750

Considérant les modèles circulaires et sphériques comme essentiels à l’harmonieuse organisation du monde, Wright considère que les étoiles se meuvent « suivant des courbes » et suggère deux méthodes de compréhension : la première admettant que les étoiles « se déplacent de la même façon, et ne dévient jamais du même plan comme le font les planètes dans leur mouvement héliocentrique autour du Soleil […] La seconde méthode pour résoudre le phénomène, est par un ordre sphérique d’étoiles, se déplaçant toutes dans des directions différentes autour d’un centre commun, comme les planètes et les comètes tournent autour du Soleil, dans une sorte de coquille, ou orbite concave ».

Thomas Wright, in On Original Theory or New Hypothesis of the Universe, London, 1750

Le système du monde selon Fontenelle, 1686, Bibliothèque de l’Observatoire de Paris

Wright précisera encore que la Voie Lactée est composée de soixante millions de mondes planétaires comme le nôtre et qu’il existe aussi d’autres systèmes semblables.

L’amplitude la vision de Thomas Wright ouvre désormais un champ beaucoup plus vaste d’investigation… auquel vont adhérer de nombreux esprits « éclairés », dont le philosophe de Königsberg Emmanuel Kant [1724-1804] qui, dans son Histoire générale et théorie du ciel de 1755, « évacue » l’idée de Dieu dans la structuration de l’univers, en conciliant les principes newtoniens avec les avancées de Wright

« On peut se représenter le système des étoiles comme un système planétaire énormément agrandi (…). L’aspect du ciel étoilé (…) reproduit en grand ce qu’est notre système planétaire (…). La Voie Lactée est, pour ainsi dire, le zodiaque de ces étoiles nouvelles ».

Emmanuel Kant, in Histoire générale de la nature et théorie du ciel, 1755

Kant imagine un centre commun, autour duquel gravitent les étoiles de la Voie Lactée et, par analogie, les nébuleuses, développant ainsi la théorie des Univers-îles, déjà énoncée par le naturaliste et géographe berlinois Alexander von Humboldt (1769-1859), dans son livre Kosmos : « L’analogie avec le système d’étoiles dans lequel nous nous trouvons, leur forme qui est précisément comme elle doit être selon notre conception, la faiblesse de la lumière nous oblige à supposer une distance infinie, tout concorde pour que nous considérions ces figures elliptiques comme de tels ordres de mondes et, pour ainsi dire comme des Voies Lactées dont nous venons de développer la constitution ; et, si ces présomptions, dans lesquelles l’analogie et l’observation concourent parfaitement à se soutenir mutuellement, ont autant de dignité que des preuves formelles, on devra tenir pour établie la certitude de ces systèmes ».

Il ajoute encore, à propos des travaux de Newton : « Newton ne pouvait (…) attester aucune cause matérielle qui pût par son extension dans l’espace du système planétaire entretenir la communauté des mouvements. Il affirmait que la main immédiate de Dieu avait réalisé cet ordre sans l’application des forces de la nature ».

Emmanuel Kant, in Histoire générale de la nature et théorie du ciel, 1755

Le principe d’analogie fonde la cosmogonie kantienne. L’origine de l’univers, après la Révélation divine initiale, est issue du chaos, lui-même succédant au néant, composé d’un état de matière décomposée et inerte. Puis se mettent en place les deux principes essentiels qui structurent l’univers : condensation et rotation, suscités – sans intervention divine – par les zones de densités inégales de la matière cosmique initiale qui, peu à peu, s’interfèrent par attraction et répulsion. Tout s’organise à partir d’un point central unique dans l’infini cosmique et demeure en perpétuelle évolution.

Au nom de ces principes de discernement et d’interférences, Kant pourra énoncer dans ce qui va devenir le manifeste de l’Aufklärung :

« L’Aufklärung permet à l’homme de sortir (Ausgang) de l’immaturité dont il est lui-même responsable. L’immaturité est l’incapacité d’employer son entendement sans être guidé par autrui.

Cette immaturité lui est imputable non pas si le manque d’entendement mais si le manque de résolution et de courage d’y avoir recours sans la conduite d’un autre en est la cause.

Sapere aude ! Aie le courage de te servir de ton propre entendement ! voilà donc la devise de l’ Aufklärung. »

Emmanuel Kant, Beantwortung der Frage : Was ist Aufklärung ?
(Réponse à la question : qu’est ce que l’Aufklärung ?) ,1784

Johann-Heinrich Lambert (1728-1777) dans son laboratoire

Le mathématicien, physicien et astronome autodidacte Johann-Heinrich Lambert [1728-1777] dans ses Cosmologische Briefe de 1761 va s’attacher, lui, à la notion d’habitabilité de l’univers, à partir de l’étude des comètes, selon le principe téléologique de finalité, opposé à la vision mécaniste, selon lequel l’univers étant parfait,  possible, il ne peut qu’être intégralement rempli par des planètes et comètes habitées, constatant que « rien dans l’univers n’est dans un repos absolu ». Son héliocentrisme nuance celui de Copernic en octroyant au soleil trois mouvements essentiels : tournant sur lui-même sur son axe, en orbite restreint, en translation vers la constellation d’Hercule. Toutes les étoiles, en mouvement constant, forment des ensembles éloignés les uns des autres, dont la Voie Lactée, hiérarchisés en systèmes qui, chacun, possède un centre exerçant une force gravitationnelle, l’ensemble des systèmes gravitant autour d’un centre unique.

[…] En Allemagne, Johann Elert Bode [1747-1826], directeur de l’Observatoire de Berlin, reprend à son compte une relation numérique liant les distances des planètes au Soleil. Au même titre que les électrons respectent des lois de distance harmoniques autour des noyaux des atomes, les planètes obéissent à une organisation analogue. La loi de Bode a un retentissement considérable au XVIIIe siècle, car elle apporte la solution une interrogation récurrente remontant à Pythagore.

Mais c’est à l’astronome, mathématicien et physicien français Pierre Simon, marquis de Laplace [1749-1827], que l’on doit, dans son Exposition du système du monde (1796), l’hypothèse décisive que notre système solaire, de même que les autres systèmes, avec leurs ensembles de planètes et de satellites, formeraient des masses nébuleuses innombrables, gravitant elles-mêmes autour d’un noyau incandescent.

« Ainsi l’on descend par le progrès de la condensation de la matière nébuleuse, à la considération du soleil environné autrefois d’une vaste atmosphère ».

Pierre Simon Laplace, in Exposition du système du monde, 1796

Laplace conjecture que certains amas de corpuscules composent des nuées de matière diffuse, au sein desquelles les étoiles peuvent se constituer par condensation.

De là il émet l’hypothèse d’une origine du monde émergée d’une nébulosité première, de structure aplatie, en rotation lente qui, en se contractant et se refroidissant, aurait fini par se fragmenter, donnant naissance à un noyau solaire incandescent, dont les vapeurs de gaz, qui s’en dégagent, créeraient des anneaux satellites, tournant en ellipses, puis qui se seraient dissolus en masses, à leur tour condensées et « fécondant » de nouvelles planètes…

« Quelle que soit sa nature, puisqu’elle a produit ou dirigé les mouvements des planètes, il faut qu’elle ait embrassé tous ces corps ; et vu la distance prodigieuse qui les sépare, elle ne peut avoir été qu’un fluide d’une immense étendue. Pour leur avoir donné dans le même sens, un mouvement presque circulaire autour du soleil ; il faut que ce fluide ait environné cet astre, comme une atmosphère. La considération des mouvements planétaires nous conduit donc à penser qu’en vertu d’une chaleur excessive, l’atmosphère du soleil s’est primitivement étendue au-delà des orbes de toutes les planètes, et qu’elle s’est resserrée successivement, jusqu’à ses limites actuelles ».

Pierre Simon Laplace, in Exposition du système du monde, 1796

La théorie « athéiste » de Laplace, imposant des lois naturelles aux doctrines physico-théologiques, chassant Dieu de sa création, ne s’imposera vraiment qu’à la fin du XIXe siècle, lorsqu’il sera démontré que de nombreuses nébuleuses, par leur spectre, s’avéraient d’origine gazeuses.

Scénario de formation du système solaire : nébuleuse primitive de Laplace. Auteur : Régis Lachaume

Mozart et le Songe de Scipion

C’est à l’âge de 15 ans que Wolfgand-Amadeus Mozart [1756-1791] compose Il sogno di Scipione, sa cinquième œuvre dramatique pour la scène. L’adolescent, auréolé de sa jeune célébrité (la création de son Mithridate avait déjà connu un grand succès à Milan), à son retour à Salzbourg  reçoit une commande adressée à son père Leopold pour célébrer le jubilé du prince-archevêque de Salzbourg Sigismund von Schrattenbach, mécène de la famille et du jeune compositeur. C’est une proposition qu’on ne peut refuser. Le sujet retenu est une adaptation théâtrale du fameux Somnium Scipionis de Cicéron, dont on a déjà dit l’influence qu’il a pu avoir sur toute la pensée antique et médiévale, spécialement dans le domaine des Harmonices mundi.

Pour l’occasion, on a repris un livret du prolifique Pietro Metastasio [1698-1782], écrit en 1735 par ce forçat du libretto, dont la morale pompeuse le style académique ne sont pas là pour soutenir l’inspiration du jeune Mozart. Mais l’ouvrage répond à des codes de circonstances et la transposition du texte de Cicéron doit satisfaire à ces exigences temporelles.

Le comte Schrattenbach ne l’entendra jamais, car il meurt soudainement à la fin de 1771. L’œuvre est alors dédiée à son successeur, le comte Hieronymus von Colloredo-Mansfeld – celui-là même qui, un plus tard, chassera Mozart de Salzbourg ! – et est créé le 1er mai 1772 au Palais de l’archevêque de Salzbourg. Cette unique représentation n’inclut qu’une seule aria, un chœur et un nouveau récitatif final pour rendre hommage à Colloredo.

L’intrigue, basée sur l’histoire originale de Cicéron, est réduite à une transcription moralisante : Scipion qui fait un rêve et s’est endormi dans le royaume terrestre de la Numidie, se réveille au Temple du paradis, où deux déesses l’approchent. L’une est la  Fortune, qui a le pouvoir de corrompre, de détruire et de créer, l’autre est la Constance, déesse de la loyauté, de la stabilité et de la vertu. Scipion, qui doit retourner sur Terre et mener son armée au combat, apprend qu il ne pourra compter que sur l’aide d’une seule des deux déesses. Tourmenté  par le doute, il choisit finalement la Constance et confirme ainsi que son cœur est pur et qu’il est un guerrier de la vérité et de la lumière.

Un récitatif final révèle que Scipion n’est autre que Colloredo, et sert de conclusion morale pour décrire la probité et les grandes vertus du nouveau Prince-Archevêque de la ville et employeur de Mozart. Ironie de l’histoire : l’archevêque avait la réputation d’être une personnalité particulièrement vénale.

Il sogno di Scipione s’écarte rarement des conventions de son époque, mais il est fascinant d’y constater la précocité du génie mozartien. Lucio Silla, son troisième opéra milanais allait voir le jour moins d’un an plus tard. L’opéra, dont il faut bien dire qu’il n’appartient pas aux œuvres majeures du compositeur, va ensuite tomber dans un long oubli …

Le récit de Cicéron est quelque peu malmené par Metastasio, au profit d’une fable morale, mais il n’est pas étonnant que Mozart y ait retrouvé les principes des justes proportions des Harmonies célestes dont son père, à l’instar de la plupart des érudits de son temps, lui avait transmis les principes lors de son enseignement. On en trouve un exemple dans ces quelques vers qui inspireront particulièrement Mozart :

LA FORTUNE
Des sphères en mouvement,
Que perçoit ton oreille ?
Aussi brillant qu’un saphir,
Au globe terrestre, que tu vois entraîné dans sa course?
SCIPION
Et quelle est parmi ces sphères, ô déesses,
Celle qui produit une si mélodieuse harmonie ?
LA CONSTANCE
Celle-ci provient de leur inégalité
Proportionnée en mouvement et en mesure.
Elles se heurtent les unes aux autres
Dans leur rotation; chacune d’elles
Rend un son distinct de l’autre
Et de toutes à la fois naît une consonance.
Bien différentes sont les cordes d’une cithare
Et pourtant lorsque la main les a accordées,
Comme il convient à l’oreille, dans l’aigu et dans le grave,
Elles donnent, une fois pincées, une douce harmonie.
Ce noeud admirable,
Cette raison mystérieuse,
Qui accorde les dissemblances,
S’appelle proportion, ordre et norme
Universels de toutes choses créées.
C’est une étincelle
Du savoir supérieur et impénétrable
Que le sage de Samos a caché dans ses chiffres.

Voici ce qu’écrit Leopold Mozart en 1751 dans son livre-méthode Versuch einer gründlichen Violinschule (l’École du violon) : « Après Pythagore vint Aristoxène de Tarente, un disciple d’Aristote. Et comme l’un basait toutes ses recherches sur le Ratio et la Proportion, et l’autre sur l’oreille, une fastidieuse querelle se développa, qui fut résolue finalement par la formule : La Raison et l’Ouïe doivent être juges en même temps. […] Entretemps, l’enseignement de Pythagore semble s’être maintenu en Grèce pendant cinq à six cents ans. Ceux qui suivaient l’opinion de Pythagore furent appelés Canonici, et les partisans d’Aristoxène furent nommés Harmonici. Depuis ce temps jusqu’à la naissance de Notre Sauveur, et après cela à peu près jusqu’à l’an 500, et même jusqu’aux environs de l’an 1000 duChrist, on a bien cherché ici ou là des choses à améliorer dans la musique : on a découvert plusieurs sons, comme la tierce majeure avec Ptolémée, et quelques sons intermédiaires avec un certain Olympus. Mais l’essentiel n’a pas été changé depuis ».

On pourrait être étonné, dans ce XVIIIe siècle préoccupé de Raison et de nouvelles découvertes géographiques et scientifiques, dans ce temps des Lumières gagné par le rationalisme, de voir les vieilles théories de l’harmonie des sphères apparaître encore bien vivantes. En fait, Mozart, comme avant lui Bach, Buxtehude ou Monteverdi, ont été baigné dans cette éducation, qui reprenait les vertus cardinales pythagoriciennes et les transmettait à travers la musique. L’enseignement des règles d’harmonie y font sans cesse références dans la plupart des traités théoriques de l’époque.

Mozart n’oubliera jamais cet enseignement, dont il trouvera un prolongement – à ses yeux essentiel – dans son adhésion à la Franc-maçonnerie, et que l’on voit sourdre souvent dans certains aspects de sa musique : attraction de certaines tonalités liées à des états d’âme particuliers, figuralismes numériques, ujtilisation symbolique du nombre 3, dialogue fréquent entre le style ancien du contrepoint et la mobilité des harmonies classiques. Sans parler de certaines séquences de ses opéras où les formules chromatiques jouent avec les dissonances, avant de les résoudre pour une sorte d’apaisement mystique (Don Giovanni, la Flûte enchantée, Cosi fan tutte, Symphonie Jupiter…)

Enfin vient La Flûte Enchantée, dont l’inspiration maçonnique est plus qu’évidente, ne serait ce que par les 3 bémols à la clé. L’opéra relate globalement le triomphe de la lumière sur les ténèbres, en s’appuyant sur la musique des sphères (acte II, scène 2) :

Celui qui chemine sur cette voie semée d’embûches
est purifié par le feu, l’eau, l’air et la terre.
S’il parvient à surmonter la peur de la mort,
il s’élèvera de la Terre vers la sphère céleste.
Ayant reçu la lumière, il sera à même
de se vouer tout entier aux mystères d’Isis.

Dans la même lignée,  Joseph Haydn [1732-1809] qui rencontrera Mozart en 1784 et entra lui aussi en Franc-maçonnerie en 1785. donnera en 1786 ses six symphonies parisiennes, en réponse à une commande, à une loge maçonnique, la Loge Olympique à Paris, où le chevalier de Saint-Georges est chef d’orchestre, et où l’on pratique et célèbre les vieilles règles des Harmonices mundi. De même, dans le prologue de son oratorio La Création (Die Schöpfung), il tentera de traduire par un accord instable de ré mineur, l’idée métaphysique du Chaos à l’origine du monde.

Deux autres illustrations du chaos:
Jean-Féry Rebel [1666-1747], Les Élémens, symphonie nouvelle, I- Le Chaos, 1738, par le Palladian Ensemble
Claude-Nicolas Ledoux [1736-1806], les Salines d’Arcs-et-Senans (à partir du chaos du péristyle du bâtiment d’entrée)

Rationalisme et incrédulité

Les temps ont changé : l’objectivation scientifique et la rationalité, issus du courant des Lumières de l’Aufklärung, au XVIIe et surtout au XVIIIe siècle, ont éloigné les esprits cherchants des Harmonices mundi : elles sont devenues de simples constructions de l’esprit. Seuls les cercles ésotériques ou occultes tenteront de perpétuer cet enseignement.

Précédé par la célèbre formule de Blaise Pascal, « Le silence éternel de ces espaces infinis m’effraie », le monde des laboratoires nouvellement créés et des cabinets de curiosité, qui vont faire l’orgueil des cours européennes, « chassant Dieu du système », ouvre l’ère de la recherche scientifique pure et dure, dépossédée des considérations religieuses et spiritualistes.

Résonnant ainsi « de concert » avec la théorie de Charles Darwin [1809-1882] sur l’évolution des espèces vivantes, les découvertes de plus en plus affinées des archéologues et philologues, déchiffrant et décryptant les monuments et annales des civilisations antiques, la cosmologie du XIXe siècle s’éloigne ainsi des récits de la Genèse, des modèles théocentriques qui prévalurent pendant des millénaires, au profit d’une description « objective » des phénomènes, corroborés par les progrès de la recherche scientifique, tel que le constate Stephan Zweig [1881-1942] dans son livre testament Le Monde d’hier :

« Le dix-neuvième siècle, avec son idéalisme libéral, était sincèrement convaincu qu’il se trouvait sur la route droite qui mène infailliblement au « meilleur des mondes possibles ». On ne considérait qu’avec dédain les époques révolues, avec leurs guerres, leurs famines et leurs révoltes, on jugeait que l’humanité, faute d’être suffisamment éclairée, n’y avait pas atteint la majorité… Cette foi en un « Progrès » fatal et continu avait en ce temps là toute la force d’une religion. Déjà l’on croyait en ce « Progrès » plus qu’en la Bible et cet évangile semblait irréfutablement démontré par les merveilles sans cesse renouvelées de la science et de la technique ».

Curieusement ce seront les artistes, au milieu d’une société de plus en plus sceptique et fonctionnelle, chosifiée par les nouvelles technologies, qui vont devenir les nouveaux dépositaires de l’Ars magna.

Vertigineuse correspondance entre physique quantique, phénomènes acoustiques et arithmétique…

On retrouve même ces formes sonores gravées dans les chapiteaux de pierre de certaines architectures : la Rosslyn Chapell, sur la colline de la Collégiale, au sud d’Edimbourg, qui fut élevée par William Sinclair, héritier d’une famille noble écossaise descendant des chevaliers Normands de Saint-Clair et, selon la légende, liée aux Chevaliers du Temple, en est un bel exemple. L’église n’est plus seulement un vaisseau de lumière et de prières, elle est un instrument de musique vibrant par chacune de ses colonnes.

Nous sommes ici au point de rencontre entre toutes les coordonnées qui font l’humain, dévoilant les rapports intimes entre les formes vivantes et les formes symboliques (rosaces, mandalas). En écho avec Pythagore, l’affirmation biblique d’un monde créé par le verbe et les méditations indiennes sur l’origine vibratoire de l’univers, la résonance ne renvoie-t-elle pas à la structure même de tout ce qui est ?

Les figures sonores de Chladni

Le physicien et musicien de Leipzig Ernst Florens Friedrich Chladni [1756-1827], né à Wittemberg, s’est beaucoup occupé d’acoustique : il imagine en particulier une méthode de mesure de la vitesse du son dans les corps solides, et fait des études sur les vibrations engendrées par le frottement d’archets de violon sur des plaques en laiton fixées horizontalement en leur centre à un socle de noyer.

Galilée avait déjà observé, alors qu’il était en train de gratter une plaque de cuivre avec des ciseaux en fer pour enlever des taches, que la plaque émettait de temps en temps un son. et qu’apparaissaient alors des lignes parallèles sur celle-ci. Il avait fait part de sa découverte dans son ouvrage Dialogue sur les deux grands systèmes du monde en 1632. En 1680, Robert Hooke avait vu, en frottant avec un archet le bord d’une plaque de verre recouverte de farine, apparaître des schémas nodaux.

Dès 1787, Chladni reprit les travaux de Hooke, en n’utilisant non plus une plaque de verre et du sable, mais une plaque en laiton saupoudrée du même sable. Il s’en suivit une série d’expériences durant lesquelles il s’efforçait de varier la fréquence du son, en changeant le point d’appui de l’archet sur la plaque ou en exerçant des points de pression sur la plaque avec ses doigts, en changeant la taille et l’épaisseur de la plaque. Il en résulta toute une série de figures de lignes nodales différentes, appelées Figures de Chladni (Klangfiguren), que Chladni va répertorier.

Les grains de sable sont éjectés des régions de la plaque où l’amplitude des vibrations est maximale (lignes ventrales), et se rassemblent le long des lignes nodales qui composent ce corps vibrant, c’est à dire les endroits où la plaque vibre le moins, là où l’amplitude est faible ou nulle. Plus il y a de lignes, ou plus elles sont rapprochées, et plus la fréquence est élevée.

Voir : quelques figures de Chladni à des fréquences précises (hertz) obtenues à partir d’une induction électrique

Ces formes géométriques « expriment » donc à une hauteur de fréquence précise (en hertz) la vibration d’un son donné. Un lien existerait donc entre l’univers des formes (géométrie) et l’univers sonore.

En 1787, Chladni a publie ses figures dans son ouvrage Entdeckungen über die Theorie des Klanges. Dès leur publication, les expériences de Chladni vont susciter beaucoup d’intérêt partout en Europe, non seulement parmi les scientifiques, mais aussi parmi le grand public. Napoléon a même invité Chladni à Paris en 1809.

à gauche : Chladni démontre sa méthode à  Napoléon, gouache (auteur inconnu)
© Porträtsammlung des Deutschen Museums, München – à droite : portrait de Ernst Chladni

Par la suite, de nombreux chercheurs ont successivement développé un modèle mathématique permettant de calculer, pour chaque plaque, les différents sons possibles, ainsi que les figures correspondantes, parmi lesquels on discerne la mathématicienne, physicienne et philosophe française Sophie Germain [1776-1831] , le mathématicien, mécanicien et astronome Joseph Louis de Lagrange [1736-1813, le mathématicien, géomètre et physicien Siméon Denis Poisson [1781-1840], les physiciens Gustav Robert Kirchhoff [1824-1887] et Lord Rayleigh [1842-1919]. Mais il faudra attendre le début du XXe siècle pour que le physicien suisse Walther Ritz [1878-1909], pionnier en physique quantique, invente une méthode utilisable en pratique pour calculer ces figures ainsi que les fréquences associées.

Ces chercheurs vont mettre en évidence les analogies entre les « images sonores » et le monde naturel, qui sont innombrables. Ça commence avec les atomes. Après tout, rien de plus logique : un atome est fait de particules élémentaires – électrons, protons, neutrons – qui sont chacune à la fois un grain de matière et une onde. L’atome est une combinaison d’ondes vibratoires qui interfèrent les unes avec les autres. Il n’est donc pas complètement étonnant que les niveaux d’énergie de l’atome correspondent aux figures d’interférences de Chladni. On sait maintenant que ces figures étranges reflètent également certaines propriétés fondamentales des nombres premiers et pourraient fournir la clé permettant de démontrer la fameuse hypothèse de Riemann, sur laquelle les mathématiciens sèchent depuis 150 ans.

Quelques liens entre les découvertes de Chladni et la CYMATIQUE (à partir du substantif grec « κῦμα » « vague »),
science de la visualisation des vibrations acoustiques © Extrait du documentaire Inner Worlds de Daniel Schmidt, 2010

Fibonacci, Bartók, Debussy et l’architecture invisible

Reprenant les lois des proportions numériques des Grecs anciens, pour lesquels le nombre était le commencement et la fin de tout, la suite de Fibonacci est ainsi une exultation numérique du nombre d’or qu’elle dissimule. La plus grande partie des espèces végétales et animales révèlent des structures développées selon cette progression de nombres : les écailles des pommes de pin pour les conifères, les graines sur le capitule des tournesols, les piquants des cactus, les écailles d’ananas, les fleurs sur le capitule des artichauts… et les formes elliptiques du nautile, comme de certains coquillages.

La suite elle-même, projetée dans l’espace, se superpose aux proportions du nombre d’or que l’on retrouve dans beaucoup de réalisations architecturales sacrées et/ou religieuses, notamment sur le fronton du Parthénon, qui s’inscrit dans un rectangle dont les dimensions des côtés adjacents sont aux proportions du nombre d’or.

Cette suite, dont chaque nombre est la somme des deux précédents (0 + 1 = 1, 1 + 1 = 2, 2 + 1 = 3, 3 + 2 = 5 etc.), se décline ainsi dans ces premiers termes :  0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144….

Ce qui a posé la pérennité et la célébrité de cette formule géniale, c’est qu’elle induit un taux de croissance exponentiel qui tend vers un ratio symbolisé par « φ », dont la valeur exacte est de (1+√5)/2, ayant comme dix premières décimales 1,6180339887… Ce rapport, considéré comme une clé de l’harmonie universelle, et qu’on nomme généralement le nombre d’or ou la proportion dorée, trouve également des représentations géométriques et architectoniques sous les formes du rectangle, du pentagone ou du triangle…

On doit cette suite numérique à Léonard de Pise, plus connu sous le nom de Leonardo Fibonacci [1175-1250], auteur de traités de mathématique et célèbre pour avoir rapporté et démocratisé la notation chiffrée indo-arabe, au détriment de la notation romaine. La logique simple et empirique de ces calculs a notamment permis d’établir un des premiers modèles mathématiques en dynamique des populations.

Quelques exemples fibonacciens : les écailles d’une pomme de pin, l’homme de Vitruve de Leonardo da Vinci,
le fronton du Parthenon, la vague de Katsushika Hokusai…

Le premier mouvement de la Musique pour cordes, percussion et célesta du compositeur hongrois Béla Bartók [1881-1945], composée en 1936 et créée le 21 janvier 1937 à Bâle par le Basler Kammerorchester dirigé par le grand mécène et chef d’orchestre suisse Paul Sacher, commanditaire de l’œuvre, est un des plus beaux exemples de construction formelle calquée sur les proportions générées par la suite de Fibonacci.

voir aussi : Bartók, Le Château de Barbe-Bleue dans Sur le fil… (in Blog-notes)

Ainsi cette fugue initiale comprend-elle en tout 89 mesures. La mesure 55/56, correspondant à la section d’or, marque le point culminant d’une progression amorcée dès le début de l’œuvre, se traduisant par une écriture de plus en plus dense et dramatique, et le point de départ d’un processus inverse en miroir decrescendo jusqu’au retour au la initial à l’unisson.

Les quatre premières entrées instrumentales correspondent aux nombres de Fibonacci. La mesure 21 marque la fin de l’énonciation du thème aux contrebasses et entame un court épisode avant l’entrée des premiers violons à la mesure 27. À cet endroit commence une transition qui mène à l’entrée de la timbale à la mesure 34, un autre nombre de Fibonacci…

Comme un système d’emboîtements, la plus petite cellule thématique, énoncée aux justes proportions, s’intègre dans les  différents segments qui, eux-mêmes répondent aux mêmes proportions, l’ensemble étant à son tour mesuré par une section dorée qui se situe très précisément au fortissimo mesure 56.

L’architecture globale, comme nombre d’oeuvres de Bartók,s’organise dans une forme en arche, favorisant une symétrie en miroir : unisson sur LA au commencement, crescendo avec acmé fortissimo en MI bémol, retour decrescendo vers LA, rendu à son unisson initial.

À cette construction extrêmement sophistiquée s’ajoute un mouvement des tonalités répondant aux attractions des pôles du cycle des quintes (qui contient le total chromatique du système tonal occidental). Le pôle initial sur LA aboutit, par modulations successives, à la section dorée sur MI bémol qui est, dans la représentation du cercle harmonique, son anti-pôle.

L’espace LA-MIb correspond à un intervalle de trois tons entiers, connu sous le nom de triton qui, lui aussi, représenta une dimension longtemps dissimulée dans le langage musical polyphonique : sa dureté et la dissonance qu’il représentait apparurent comme impropres à soutenir la parole de Dieu. Il fut même qualifié de Diabolus in musica et ne pouvait dès lors se concevoir que dans sa résolution naturelle vers la quinte juste, présente naturellement dans le système des proportions pythagoriciennes.

Mais l’attraction de cette attirance des notes du cycle des quintes vers leur anti-pôle ne put que séduire nombre de compositeurs, qui prirent un malin plaisir à dissimuler cet intervalle dans certaines de leurs oeuvres…

On retrouve, par exemple, ce triton dans le thème initial du Prélude à l’après-midi d’un faune de Claude Debussy,énoncé par la flûte sans soutien harmonique, procurant aussitôt à l’oreille une mobilité et une impression de flottement qui ne pouvaient que séduire un compositeur aussi novateur. Ne souhaitait-il pas délester ainsi ce poème inspiré des vers de Mallarmé du schéma tonique-dominante-tonique issu du vieux modèle tonal classique.

Revenons à Bartok. Comme nous avons pu l’expliquer sommairement, à une dynamique horizontale (Fibonacci) répondent une cosmologie harmonique (cycle des quintes) et une forme globale en miroir, qui donnent à cette pièce relativement courte un plan achevé, une architecture invisible. En l’occurence, une oreille, même non informée de ces éléments très savants, peut percevoir l’équilibre qui émane cette musique. Selon la formule de Rameau, l’art est caché par l’art même…

Scriabine le visionnaire

Pour Alexandre Scriabine [1872-1915], l’harmonie cosmique ne peut que réunir, dans une même communion vibratoire, les sons et les couleurs. Compositeur et pianiste russe né à Moscou, porté vers les notions d’absolu ancrées dans une vision syncrétique mêlant philosophie, symbolisme, occultisme, théosophie, pour lui « le monde est un système de correspondances à la fois immobile à chaque instant donné et se transformant inlassablement dans le temps » : c’est dans une fusion, à la fois sonore, visuelle et mystique, que peut se reconstituer l’Un, le Tout.

« La vibration, écrit-il, relie les états de conscience entre eux et constitue leur seule substance ». Et d’ajouter : « Il n’y a pas d’espace et de temps en dehors de la sensation. Il n’y a pas d’espace et de temps donnés qui préexisteraient aux sensations, lesquelles y seraient incluses. L’espace et le temps sont créés en même temps que les sensations ».

Il ajoute dans ses Cahiers que « dans la forme de la pensée l’extase est la plus haute synthèse. Dans la forme du sentiment l’extase est la plus haute béatitude. Dans la forme de l’espace l’extase est le plus haut épanouissement et l’anéantissement. En général, l’extase est le sommet, est le dernier instant, qui en tant que phénomène n’existe qu’en relation avec les autres phénomènes et résume toute l’histoire de l’humanité. »

Dans son Poème de l’extase, par exemple, on trouve la présence récurrente du nombre 36 dans les différentes sections de l’œuvre, du double tétrakys pythagoricien (1+3+5+7 et 2+4+6+8) qui, selon Platon, symbolise l’harmonie universelle.

Par rapport à l’ensemble de la pièce, le nombre d’or (la fameuse proportion « divine ») mesure très exactement la séparation de la première à la deuxième partie au niveau de la réexposition à la mesure 375 et se retrouve d’autre part dans le plan de la « luce », où il distingue les séquences de bleu pur (début et fin) des autres couleurs du spectre, réparties sur 374 mesures !

« L’océan de la fantaisie crée : cela signifie qu’il colore ses gouttes de différentes teintes, cependant il lui suffit d’en colorer une parmi les autres de quelque couleur que ce soit, les autres, immanquablement recevront d’autres couleurs correspondantes, car aucune couleur n’existe en dehors du rapport avec les autres couleurs. Ceci donne une certaine idée par analogie de la création individuelle et de son action sur l’univers. » (Cahier II, §93)

Sur le plan harmonique, il crée un « accord synthétique », composé de six quartes superposées (do-fa dièse-si bémol-mi-la-ré), issu lui-même du cycle des quintes, qui contient tout le système tonal à 12 demi-tons.

Recherchant l’état d’extase où le son-couleur est généré par la vibration – « Un ensemble complexe et précis de vibrations : tel est le but d’une œuvre », note-t-il encore dans ses Cahiers, avant de préciser : « Dans le mouvement vibratoire, les points extrêmes de chaque oscillation sont des moments et peuvent être perçus seulement en tant que limites du mouvement vibratoire […]. C’est par là que s’explique ce fait que chacun des états existe seulement dans le système de relations, et en dehors de lui est impensable » – il tente de fixer des correspondances sonores et colorées pour chacune des 12 notes du système tonal, liées à des états d’âme prédisposant à un programme mystique.

Cercle chromatique des correspondances sonores et colorées d’après Scriabine
conception, réalisation : © Patrick Crispini, in La Vibration originelle

Prolongeant des préoccupations déjà présentes dans la « Gesamtkunstwerk » (l’œuvre d’art total) souhaitée par Richard Wagner pour ses opéras, en accord avec les démarches syncrétiques très en vogue dans les milieux esthétiques et philosophiques à la fin du XIXe siècle, il envisage toutes sortes de « scénarios divins » (sic) pour que tous les sens soient mis à contribution pendant l’exécution de l’œuvre, ouïe, vision, toucher, odorat… réunis dans une forme de chorégraphie collective portée par les vibrations.

Ainsi la partition de Prométhée ou le Poème du Feu, composée en 1910, installe, sans doute pour la première fois dans l’histoire de la musique, un « conducteur » spécifique pour la « luce » (la lumière).

Porté par sa vision synoptique, avec le peintre symboliste Jean Delville, auteur de la page de titre de Prométhée, ébauchée en 1908-1909 à Bruxelles, il prévoit pour son « grand Œuvre », dont la résurrection du vieux mythe prométhéen indique bien l’inscription dans une tradition antique et ésotérique, un clavier de lumière,  où chaque touche du clavier correspondrait à une couleur, actionné par un instrumentiste parmi les autres musiciens de l’orchestre, permettant de projeter une lumière colorée diffuse en symbiose avec le flux musical.

Mais, en 1913, le dispositif prévu, entraînant des problèmes sans fin, est abandonné et Scriabine ne pourra jamais voir l’accomplissement de sa « vision ». Scriabine tombe brusquement malade. Il trouve la force de donner un dernier concert en avril et meurt de septicémie, après de terribles souffrances, le 27 avril 1915.

Cette même année, une création de l’œuvre a lieu au Carnegie Hall sous la direction de Serge Koussevitsky, au cours de laquelle un clavier de couleur, appelé chromola, fabriqué spécialement pour l’occasion par Preston Millar, un ingénieur des laboratoires Bell, permettait de projeter des couleurs sur un écran, la frappe des touches du clavier déclenchant, via un circuit électrique, l’allumage d’une lampe de couleur. Mais les effets obtenus sont très éloignés du bain vibratoire englobant exécutants et auditoire et du « transport » métaphysique que préconisaient Scriabine.

Depuis, de nombreuses tentatives d’exécutions colorées ont eu lieu un peu partout dans le monde, mais le résultat demeure décevant, malgré les nouveaux moyens de réalisations numériques assistées par ordinateur. Le plus souvent, le « plaquage » du programme coloré se rapproche plus d’effets artificiels proches de ceux que l’on pourrait voir dans un cabaret ou une boîte de nuit, et dont la vulgarité, c’est le moins que l’on puisse dire, dessert plus l’esprit de l’œuvre qu’elle ne la magnifie… On attend toujours une réalisation digne de ce nom, où le substrat technologique puisse se fondre dans une osmose vibratoire profonde et absolue, où la lumière et le son ne fassent plus qu’un. Une utopie ? …

Extrait de la partition d’orchestre de Prométhée, le poème du feu (partie instrumentale de la Luce surlignée en jaune).
conception, réalisation : © Patrick Crispini, in La Vibration originelle

Le point d’orgue de cette quête devait être la liturgie sacrée de son œuvre ultime : le Mystère, projet initié à la suite de la rencontre à Londres du philosophe musicien indien Inayat et des milieux théosophiques de cette ville. Malheureusement, l’ouvrage ne fut jamais écrit et seuls en subsistent le livret poétique, le « programme » mystique et 53 pages d’esquisses musicales de l’Acte Préalable, dont la fonction de « rituel préparatoire » aurait dû précéder le Mystère proprement-dit.

« Il n’y aura pas le moindre spectateur. Tout le monde sera participant. La performance exige des gens spéciaux, des artistes spéciaux et une culture complètement nouvelle. Le personnel inclut un orchestre, un grand chœur mixte, un instrument avec des effets visuels, des danseurs, un cortège, de l’encens et l’articulation du rythme et des autres sens. La cathédrale dans laquelle il aura lieu ne sera pas un bâtiment de pierres homogènes, mais changera continuellement avec l’atmosphère et le mouvement du Mysterium. Cela sera fait à l’aide des brumes et des lumières, qui modifieront les contours architecturaux. »

La durée totale de l’œuvre devait s’étendre sur sept jours et son exécution se dérouler dans un temple sphérique installé sur les contreforts de l’Himalaya ou dans le parc de la Société théosophique à Adyar en Inde.

Dessin de la main de Scriabine, le Temple-sphère pour Mysterium

L’harmonie et l’orient

Ces visions harmonieuses sont-elles si différentes de celles de la Chine ancienne, voire de toute l’Asie orientale ? L’harmonie chinoise porte le nom de he, prononcé wa en japonais.
Le caractère se compose de la céréale et de la bouche, autrement dit de la matière et du son vibratoire.

« Ô sagesse profonde, ancrée dans la matière ! » écrit Lao Tseu.

Le terme he apparaît dans les inscriptions sur bronze du VIIIe siècle avant notre ère et dans les Classiques. Comme notre mot harmonie, il signifie l’état de concorde : il entre ainsi dans la composition du terme heping, qui signifie la paix. Mais il désigne aussi la vertu qui permet de créer ou perpétuer l’état d’harmonie, ainsi que l’action d’harmoniser.

Dès les inscriptions les plus anciennes, on le trouve appliqué à l’accord des instruments de musique. L’harmonie chinoise est donc, elle aussi, intimement liée à la musique. Elle l’est également à une science des nombres et des rapports de nombres qui mesurent instruments de musique et intervalles musicaux, et les mettent en relation avec le cycle du calendrier et des astres. L’essence de l’harmonie est bien définie au chapitre de l’Invariable milieu des Mémoires sur les rites.

« Tant que joie, colère, tristesse ou plaisir ne se sont pas manifestés, cela s’appelle le Milieu [c’est-à-dire pure efficacité de l’énergie vitale]. Quand ces sentiments naissent mais restent dans les justes limites, on dit qu’il y a harmonie. Le Milieu est le grand fondement de l’univers, et l’harmonie est la voie qu’il doit suivre. Quand le Milieu et l’harmonie atteignent partout leur plus haut degré, chaque chose est à sa place au ciel et sur la terre, et tous les êtres naissent et prospèrent ».

L’ordre cosmique conjugue dans l’espace et le temps une alternance d’aspects contrastés et complémentaires, dont le yin et le yang sont la figure originelle. L’intuition semble rejoindre celle de Jean Scot Érigène, clerc et philosophe irlandais du IXe siècle :

est enim harmonia dissimilium inaequaliumque rerum adunatio
(l’harmonie est en effet la réunion, la mise en un tout de réalités différentes et inégales).

Dans la tradition chinoise, une célèbre légende évoque comme suit la création des douze sons étalons :

« Huangdi ordonna à Linglun de faire les règles de musique. Linglun se rendit à l’ouest des monts Daxia, sur le flanc nord du Ruan Yu ; dans la vallée d’une petite rivière il trouva des bambous droits et à la cavité intérieure large ; en coupant entre deux nœuds, il obtint une longueur de 3,9 pouces dans laquelle il souffla, émettant la fondamentale de Huangzhong. Il fit ensuite douze tubes. Redescendant du Ruan Yu, il entendit le cri de phénix mâle et femelle, émettant les douze notes chromatiques : le mâle en chantait six, la femelle les six autres. Ces sons étaient accordés au Huangzhong : la fondamentale de Huangzhong permettait de les engendrer. C’est pourquoi il est dit « la fondamentale de Huangzhong est la racine des douze notes chromatiques ». Huangdi ordonna aussi à Linglun et Rongjiang d’accorder douze cloches qui devaient s’accorder aux cinq sortes de sons, pour utiliser lors des danses « Ying » et « Shao » ; au deuxième mois du printemps, au jour marqué du 16e binôme du cycle sexagésimal, jour marqué « gui », il ordonna que l’on nomme [le carillon] « étang du 31e hexagramme ». 

Lü Buwei [v. -300 -v. -236 av. J.C], Lü shi Chunqiu Zhong Xia ji Guyue
(Musique ancienne, Dit de Zhongxia, Printemps et Automnes de maître Lü)

Le diapason ainsi devint déterminant : seul l’empereur le détenait. Régulièrement il allait écouter les orchestres de ses provinces et vérifier qu’ils ne déviaient du diapason unitaire, les écarts au diapason impérial (consonance) étant signe avant-coureur d’agitation sociale et de trouble (dissonance). La remise dans le droit chemin s’effectuait comme un réajustement au son de référence (ajuster = harmoniser).

Au-delà de la légende, c’est dans l’observation de la mobilité du ciel, du mouvement des astres autour d’un pôle fixe, qu’on trouve l’origine des principes de référencement à une note étalon. La tradition parle de « faire tourner le gong » autour du shang, afin de déterminer les hauteurs absolues et les hauteurs relatives. Ainsi le mode pentatonique chinois [五聲 wusheng] est une échelle d’intervalles fixes de cinq notes où, à partir de la position de la note initiale [宫 gong], se déduisent les quatre autres : 商 shang, l’intervalle de seconde, 角 jue la tierce, 徵 zhi la quinte, 羽 yu la sixte.

Le système pentatonique wusheng

Oiseau mythique emblématique de l’histoire de l’humanité, vénéré par de nombreuses cultures égyptienne, grecque, chinoise, arabes… le phénix, dans la culture traditionnelle chinoise, est appelé feng huang. Il ne désigne pas un seul oiseau, mais deux : Feng, qui représente l’oiseau mâle, huang l’oiseau femelle. Ensemble, ils forment une métaphore du symbole du yin et du yang. Plus tard, le feng et le huang seront rassemblés en un seul oiseau femelle et souvent associé au dragon.

Le feng huang a joué un rôle primordial dans la création du cosmos. Pan Gu, dieu de la création, serait le premier être vivant issu de l’œuf du chaos, suivi par les autres incarnations appelés esprits : le dragon qilin (animal chimérique à tête de dragon, un corps de cerf recouvert d’écailles de poisson avec une corne sur la tête), une tortue et un phénix (feng huang), qui sont à l’origine de la création de l’univers.

Le feng huang est considéré comme un symbole de grâce, de vertu et de révélations (auspices) et de chance (dans le feng shui). Rapportés par Hérodote [484-425 av. J.-C.], les prêtres d’Héliopolis prétendaient que le phénix vivait 500 ans, puis construisait un bûcher, composé de myrrhe et de cannelle, d’où surgissait sa progéniture avant de s’envoler. En Égypte ancienne, le phénix, sous le nom de Bennu, apparaissait sous la forme d’un héron, qui vivait au sommet des pierres de ben-ben (pierres sacrées du temple solaire d’héliopolis) ou d’obélisques et était vénéré aux côtés d’Osiris et de Râ. Bennu était considéré comme un avatar d’Osiris, un symbole vivant de la divinité.

Revenons maintenant à la légende de Ling lun. Que nous transmet-elle d’essentiel, au-delà de la transcription poétique, si l’on tente d’en déceler les clés symboliques en regard des éléments de chaos et d’harmonie que nous avons déjà eu l’occasion de mettre en valeur dans d’autres allégories ? Le maître de musique est chargé d’une mission de la plus haute importance : trouver un moyen vibratoire d‘ajuster le disparate de l’univers. Pour cela il va utiliser le bambou, dont le symbole naturel est la plénitude sur le néant, car il croît autour du vide, ce qui est pour les sagesses orientales le le centre subtil du développement spirituel. Ces noeuds le mesurent et sa solidité le rend sufisamment souple pour ployer mais ne jamais se briser (« qui se plie restera entier, qui s’incline sera redressé, qui se tient creux sera rempli, qui subit l’usure se renouvellera », Lao Tseu, in Tao Te King). C’est le support idéal, résistant et humble, puisque son coeur est vide – pour le travail qui est demandé au maître de musique. Du bambou, issu des eaux (chaos), va naître le son fondamental (Huangzhong) grâce à la coupe précisément effectuée entre les noeuds (proportions, voir aussi : monocorde  pythagoricien), puis de cette première coupe les autres flûtes (intervalles, harmoniques). Le chant des deux phénix, mâle et femelle, oiseaux eux-même venus de l’oeuf originel du chaos (feu) permettra de confirmer la justesse de l’échelle chromatique ainsi obtenue (ajuster = harmoniser).

Parcours symbolique à travers les quatre éléments et la voie spirituelle du chaos à l’harmonie qui résonne en similarité avec la doctrine grecque pythagoricienne : de l’eau (bambou) à l’air (les flûtes), par le passage du feu (phenix = renaissance), la musique peut ainsi se répandre sur la terre pour devenir le maître-étalon vibratoire par lequel l’empereur pourra établir la légitimité de son règne.

Les questions touchant au monde vibratoire, et plus sensiblement au domaine de la résonance, trouvent dans l’expression ganying une synthèse qui plonge ses racines dans la plus haute antiquité chinoise, qui connait son épanouissement sous la dynastie des Han occidentaux [206 av. J.-C.-9 apr. J.-C.]. On peut traduire l’idiome Ganying par les binomes « action/réaction »,« stimulus/réponse », « affect/effet » et plus précisement par le concept de « résonance ».

Quand l’accordeur de luth touche la corde gong sur un instrument,
la note gong sur l’autre instrument résonne ;
quand il pince la corde jue sur un instrument,
la corde jue sur l’autre instrument vibre.
Ceci résulte du fait que des notes semblables sont en harmonie mutuelle.
Supposons maintenant que l’accordeur modifie l’accord d’une des notes,
de telle sorte que celle-ci ne corresponde à aucune des cinq notes
et que, lorsqu’il la frappe, les vingt-cinq cordes se mettent à résonner :
dans ce cas on a suscité un son indifférencié
qui gouverne toutes les notes musicales.
Ainsi celui qui communique avec l’harmonie suprême divague comme un homme parfaitement ivre ;
il s’abandonne aux douceurs d’un sommeil où il erre et s’ébat, sans qu’il sache comment il est parvenu à cet état.
S’enfonçant dans une agréable moiteur, s’abîmant dans une molle hébétude,
il est comme s’il n’avait pas encore commencé à émerger de son origine.
Tel est ce qu’on appelle la grande communication.

Huainan zi, IIe siècle av. J.C.

D’une manière plus générale, le principe de Résonance réside dans celui de Beauté, au coeur du Yi.

Comme le note l’écrivain, poète et calligraphe François Cheng dans Cinq méditations sur la beauté paru en 2008 : « À sa base, l’idéogramme yi désigne ce qui vient de la profondeur d’un être, l’élan, le désir, l’intention, l’inclination. Il se combine avec d’autres caractères mais les surplombant tous yi-jing signifie « état supérieur de l’esprit, dimension suprême de l’âme » […] C’est dans la mesure où le yi, dans une oeuvre particulière, atteint son plus haut degré, jusqu’à résonner en harmonie avec le yi universel, que cette oeuvre acquiert sa valeur de plénitude et de beauté. Le yi-jing en question, outre son sens d’ « état supérieur de l’esprit, dimension suprême de l’âme », signifie alors « accord, entente, communion ». Aux yeux d’un Chinois, la beauté d’une chose réside donc dans son yi , cette essence invisible qui la meut. C’est le yi qui est sa saveur infinie, qui n’en finit pas de susciter parfum et résonance. »

La théorie des cordes

Aujourd’hui la théorie des cordes remet les principes d’un univers vibratoire au goût du jour. Celle-ci propose d’unifier les quatre interactions fondamentales, en décrivant toutes les particules élémentaires comme des différents états de vibration d’une corde.

Si les physiciens théoriciens se penchent avec fascination sur cette idée depuis trente ans, c’est parce qu’elle permet de réconcilier la théorie de Relativité Générale d’Einstein, qui décrit notre univers aux échelles astronomiques, avec les principes de la Mécanique Quantique qui régissent le comportement de la matière aux échelles microscopiques. La théorie des cordes est-elle en voie de réaliser le songe de Scipion initié par les pythagoriciens, d’une description ultime de la nature, qui permettrait de retrouver toutes les lois connues de la physique, ainsi que les valeurs des constantes fondamentales, par un processus de pure déduction logique ? Aurons-nous un jour une confirmation expérimentale directe de la structure supposée cordiste de la matière ?

Dans la théorie des cordes, les particules élémentaires que nous observons dans les accélérateurs particulaires peuvent être comparées à des notes de musique ou à des modes d’excitation de cordes élémentaires.

Les physiciens et mathématiciens semblent très intéressés par les implications de cette théorie : tout en fournissant une explication du comportement connu de particules comme les électrons et les protons, elle donne une description de la gravitation en termes de comportement de cordes vibrantes ayant la forme de boucles. De nombreux physiciens estiment que les supercordes constituent donc le meilleur espoir de pouvoir développer un jour une « théorie du tout » fondamentale.

Robert Fludd, Utriusque Cosmi Historia, Sensorium dei : l’univers conçu comme monocorde, Oppenheim, 1617

Robert Fludd [1573-1637], polygraphe né à Milgate, dans le comté de Kent. Tôt il quitta le métier pour l’étude des lettres et des sciences, la philosophie, la théologie, la médecine, les sciences naturelles, et surtout l’alchimie et la théosophie. ayant passé une bonne partie de sa vie à voyage il devint un des hommes les plus érudits et célèbres de son temps Il se fit recevoir docteur en médecine à l’université d’Oxford, et s’établit à Londres.

La symphonie du monocorde du monde ou monocorde céleste est un monocorde pythagoricien actionné par la main de Dieu : sur la division de sa corde on trouve les proportions engendrant les notes de la gamme (indiquées en lettres selon le système anglo-saxon). De bas en haut sont mis en vibration les 4 éléments, puis les « planètes » et enfin les zones paradisiaques.

En guise de conclusion : la quête d’harmonie…

Nous l’avons vu, toute les définitions du mot se rejoignent sur l’idée que cet état particulier d’équilibre ne peut émerger que d’un chaos préalable, d’une séparation entre une aspiration vers la beauté, la sérénité, l’épanouissement de l’être, et la remise en question, l’anéantissement des certitudes, ce qu’on pourrait appeler le doute.  Il ne faut donc pas craindre de vivre pleinement ces contradictions, ces tiraillements, ces déchirements, ces tâtonnements, indispensables à la construction de la maison « homme ». Quel que soit la qualité du propos, le discours conserve son sens de discors, de discordance, qui l’éloigne d’autant de la concordia, de l’harmonie. La solution ne vient donc pas du langage, aussi brillant soit-il.

Le message que nous livrent les racines étymologiques du mot, les métaphores du mythe, ne laissent aucune place au doute : l’harmonie ne peut pas naître du discours, de l’art du verbe. La recherche de l’harmonie ne peut surgir que d’un cheminement intérieur, solitaire, individuel. N’oublions pas les leçons du mythe : après l’ajustement initial, il faut réunir la lyre d’Hermès, le collier d’Héphaïstos et la voie de Cadmos tournée vers l’Orient, pour donner naissance à l’alphabet, à la communication

« Ce qui est taillé en sens contraire s’assemble ;
de ce qui diffère naît la plus belle harmonie ;
tout devient par discorde »

rappelle Héraclite.

Pour se réajuster [harmonein], à partir du chaos vers un nouvel équilibre pouvant conduire à l’harmonie, plusieurs voies s’offrent au cherchant, un enseignement étant à puiser dans l’ordre cosmique des Harmonices mundi.

La musique, qui est la transposition des nombres et des proportions dans le monde vibratoire, détient les clés des résonances qui ordonnent et ajustent sans cesse les mouvements cosmiques et biologiques, comme les harmoniques vibrent à l’infini selon l’amplitude des fréquences et produisent les formes du vivants.

L’harmonie apparaît donc, au-delà du langage, comme une dissolution de l’être revivifié, par la musique, par le feu, dans la vibration universelle, l’Harmonie divine ou, si l’on préfère, dans la proportion parfaite.

L’univers étant silencieux à l’oreille humaine, il faut, pour l’entendre vibrer, l’accueillir en nous et pour cela, créer ce vide auquel nous convient toutes les sagesses immémoriales.

Pour cela il faut réapprendre la décantation de nous-même, l’abandon des pesanteurs, la clairvoyance, telle que nous l’enseigne l’art du vitrail.

« Le son musical, par le mouvement de l’air, déplace le corps : 
au moyen de l’air purifié il excite l’esprit aérien, 
qui constitue le lien entre le corps et l’âme, 
au moyen de l’émotion il agit sur les sens et, en même temps, sur l’âme »

écrit Marcile Ficin, dans son traité De vita cœlitus comparanda (Comment organiser sa vie de manière céleste), paru en 1489.

La musique, encore une fois, nous donne la clé : sur un instrument à cordes, pour produire un harmonique à partir d’un son fondamental, il faut laisser vibrer la corde à vide.

Il en est de même de la colonne d’air des instruments à vent.

« Dans l’espace d’un bref instant, et lors d’une vraie contemplation méditative, je remarquais que dans une sonate, chaque passage du majeur au mineur, chaque transformation d’un mythe ou d’un culte, chaque formulation classique ou artistique ne doit être rien d’autre que le chemin vers le centre du secret du monde, où le sacré se manifeste à jamais entre le va-et-vient de l’inspiration et l’expiration, entre le Ciel et la Terre, entre Yin et Yang »

note Hermann Hesse dans son livre Das Glasperlenspiel (Le Jeu des perles de verre).

Face à ce grand mystère de l’univers, de nombreuses thèses ont fleuri et continuent à diviser le monde la science. Les courants empiristes ne voient dans le modèle mathématique qu’un processus d’abstraction, une sorte de poétique du nombre et des équations sans autre lien avec la réalité qu’une construction intellectuelle. Les philosophies issue du neoplatonicisme considèrent les objets mathématiques comme des idéalités qui ont servi de modèles à la constitution des phénomènes naturels. La lignée issue de la pensée kantienne et de l’Aufklärung ne peut envisager d’appréhender les phénomènes de la nature hors des structures fondées sur l’identification à l’être humain : « les formes à priori de la sensibilité » à travers l’espace, le temps, l’entendement constituent les conditions de toute expérience physique, et donc de toute hypothèse mathématique. D’autres encore réfutent tout mystère dans le constats des phénomènes métaphysiques numériques, puisque les mathématiques ne représentent qu’une abstraction symbolique livrée à l’aléatoire des interprétations. Ils ne voient dans les démonstrations liées au Harmonices mundi que des élucubrations plus ou moins fantaisistes, plus ou moins scientifiques, romanesques… voire absurdes.

Au-delà de ces débats souvent stériles, les biologistes, les entomologistes, munis de la technologie la plus sophistiquée, observent et rapportent des milliers d’exemples qui confortent étonnamment cette dynamique unitaire présente dans le monde vivant : les essaims d’abeilles, depuis toujours, ne savent-elles pas construire des nids dont la structure hexagonale permet d’aménager le maximum d’alvéoles pour un minimum de cire. Cette propriété, déjà conjecturée au IVe siècle, ne fut démontrée qu’en 1999 sous le nom de théorème du nid d’abeille. L’observation de la formation des ouragans, des galaxies et même la division de la cellule ne confirme-t-elle pas cette synchronie ? La forme d’un œuf ou d’un chou romanesco ? La spirale des graines de tournesols ou celles des marguerites ? La suite de Fibonnaci dans les pommes de pin, dans l’enroulement de la queue des caméléons ou du mille-pattes, des chenilles ou des fougères, dans la coquilles du nautile ou de l’escargot… et même dans la configuration de nos empreintes digitales ?

Ne vient-on pas de détecter chez le moustique Aedes ægypti que mâles et femelles avec leurs ailes se livraient à un duo musical comme une sorte d’accord tacite avant accouplement ? « La plupart des sons sont en effet composés de plusieurs types de fréquences : la fondamentale – la fréquence la plus basse du son, celle qui constitue en quelque sorte la « note » – et les harmoniques – des sons dont la fréquence est deux fois, trois fois (etc.) plus élevée et l’intensité moins forte que celle de la fondamentale. Ainsi, pour la femelle, si la fondamentale est d’environ 400 Hz, les harmoniques seront d’environ 800 Hz et de 1200 Hz. De même, si la fondamentale de son mâle est de 600 Hz, les harmoniques seront de 1200 Hz et de 1800 Hz. Dans les deux cas, une fréquence proche de 1200 Hz apparaît. Or, d’après les chercheurs, lorsqu’un mâle et une femelle sont en présence, ils se mettent à moduler la vitesse de leurs battements d’ailes jusqu’à produire exactement la même fréquence harmonique, celle située aux alentours de 1200 Hz. Cette synchronisation n’a cependant pas lieu lorsque la femelle a d’ores et déjà été fécondée par un mâle. Par ce système de communication, les mâles pourraient ainsi détecter très facilement les femelles qu’il reste à féconder, ce qui accroît le succès reproducteur de l’espèce » (in Le Blob extra-media, Cité des sciences, Paris). Ce bzzz, qui nous irrite tant, serait pourtant le comportement très sophistiqué d’une harmonie recherchée et synchronisée, une convergence harmonique, véritable  conversation entre les sexes.

La bioacoustique enregistre les ondes sonores émises par des végétaux terrestres ou aquatiques. Elle a démontré que des variations dans les taux de germination, de croissance, d’immunité de végétaux sont réactives à certaines fréquences, que les plantes détectent leurs voisines à travers des signaux de communication par des phytochromes, et qu’elles peuvent utiliser le son comme moyen d’investiguer leur environnement . La sève qui monte dans les troncs d’arbre ne produit-elle pas une sorte de crépitement décelable grâce au progrès des moyens de captation, et les racines de même qui répondent aux ondes sonores émises à des fréquences correspondant aux ondes qu’elles émettent elles-mêmes ? L’observation de ces transductions des vibrations sonores en signaux capables de provoquer des modifications comportementales ne révèle-t-elle pas une forme de communication souterraine, invisibles, pour une grande part, nous échappe très largement ?

Pour conclure, citons encore Galilée : « La philosophie est écrite dans ce vaste livre qui constamment se tient ouvert devant nos yeux (je veux dire l’Univers), et on ne peut le comprendre si d’abord on n’apprend pas à connaître la langue et les caractères dans lesquels il est écrit. Or il est écrit en langue mathématique, et ses caractères sont les triangles, les cercles et autres figures géométriques, sans lesquelles il est humainement impossible d’en comprendre un seul mot, sans lesquelles on erre vraiment dans un labyrinthe obscur. » (Galileo Galilei, in Il Saggiatore, 1623)

Sur son chemin de vie, entre chaos et harmonie, qui nécessite sans cesse le réajustement aux justes proportions, à l’instar des voies de connaissance que montrent la plupart des sagesses du monde, l’être humain est une caisse de résonance de l’univers.

Il possède ses harmoniques :
encore faut-il qu’il puisse les libérer et que nous sachions les entendre…